661 L*IBER* S*TATICÆ*
4 DEFINITIO.
Gravitati centrum eſt ex quo, vel ſola cogitatione,
ſuſpenſum corpus quemcumque ſitum dederis, illum re-
tinet.
ſuſpenſum corpus quemcumque ſitum dederis, illum re-
tinet.
DECLARATIO.
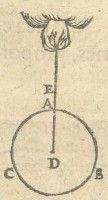
ABC globus eſto, æquabili ubique &
materiâ &
pondere,
 3[Figure 3]
quem cogitatione noſtra ex centro D, lineâ E D ſuſpenſum
3[Figure 3]
quem cogitatione noſtra ex centro D, lineâ E D ſuſpenſum
fingamus, qui quoquo modo verſatus, motusq́ue, quem de-
deris ſitum, retinebit, ſi enim B ad locum A aliæq́ue partes
alio transferantur immotæ manebunt, ſecus materia inæqua-
bilis eſſet, & alio loco denſior graviorq́ue, alio verò rarior &
levior, quod contra theſin eſſet. D itaque, ex definitionis ſen-
tentia, centrum gravitatis fuerit globi A B C. Idem judicium
deomnibus eſto, nullum enim non corpus inordinatæ figuræ
& materiæ inæquabilis gravitatis ſit ſive figuræ ordinatæ, &
æquabilis gravitatis, hujuſmodi punctum habet, à quo ſuſpenſum eandem po-
ſitionem ſervat quæ data fuit, quod gravitatis centrum appellatur. Vt autem
ſuis proprietatibus magis innoteſcat hoc addemus. Gravitatis centrum in cor-
poribus, ut columnis, ſphæris ſphæroïdibus, & quinque ordinatis, & c. ſi ſunt
ex materia æquabiliter ubique ponderoſa, idem eſt cum figuræ vel magnitu-
dinis puncto quod Geometricè centrum appellatur. Corporum vero inæqua-
biliter ponderosâ hæc puncta magnitudinis & gravitatis eodem loco non ha-
bent. In pyramidibus enim, & inordinatis ſolidis non magnitudinis centrum,
ſed gravitatis tantum eſt. Multa etiam corpora ſunt, ut annuli, unci, pelves, &
alia hujuſmodi, quæ gravitatis centrum, non intra verũ extra materiam habĕt.
fingamus, qui quoquo modo verſatus, motusq́ue, quem de-
deris ſitum, retinebit, ſi enim B ad locum A aliæq́ue partes
alio transferantur immotæ manebunt, ſecus materia inæqua-
bilis eſſet, & alio loco denſior graviorq́ue, alio verò rarior &
levior, quod contra theſin eſſet. D itaque, ex definitionis ſen-
tentia, centrum gravitatis fuerit globi A B C. Idem judicium
deomnibus eſto, nullum enim non corpus inordinatæ figuræ
& materiæ inæquabilis gravitatis ſit ſive figuræ ordinatæ, &
æquabilis gravitatis, hujuſmodi punctum habet, à quo ſuſpenſum eandem po-
ſitionem ſervat quæ data fuit, quod gravitatis centrum appellatur. Vt autem
ſuis proprietatibus magis innoteſcat hoc addemus. Gravitatis centrum in cor-
poribus, ut columnis, ſphæris ſphæroïdibus, & quinque ordinatis, & c. ſi ſunt
ex materia æquabiliter ubique ponderoſa, idem eſt cum figuræ vel magnitu-
dinis puncto quod Geometricè centrum appellatur. Corporum vero inæqua-
biliter ponderosâ hæc puncta magnitudinis & gravitatis eodem loco non ha-
bent. In pyramidibus enim, & inordinatis ſolidis non magnitudinis centrum,
ſed gravitatis tantum eſt. Multa etiam corpora ſunt, ut annuli, unci, pelves, &
alia hujuſmodi, quæ gravitatis centrum, non intra verũ extra materiam habĕt.
In definitione, vel ſolâ cogitatione, dicitur, quod in definitioneilla poni de-
bent, quæ definiti naturam maximè declarant, quod & in Pappus 8 lib. ubi
gravitatis centrum definit, cogitatione commodiſſime fecit. Etiam iſto pacto
definire licet: Gravitatis centrum eſt, per quod plana quavis ducta corpus in duas
partes aquilibres dividunt. Quid autem æquilibritas ſive ęquipondium ſit 11 de-
finitione dicitur.
bent, quæ definiti naturam maximè declarant, quod & in Pappus 8 lib. ubi
gravitatis centrum definit, cogitatione commodiſſime fecit. Etiam iſto pacto
definire licet: Gravitatis centrum eſt, per quod plana quavis ducta corpus in duas
partes aquilibres dividunt. Quid autem æquilibritas ſive ęquipondium ſit 11 de-
finitione dicitur.
5 DEFINITIO.
Gravitatis corporeæ diameter eſt recta infinita per gra-
vitatis centrum acta: Et gravitatis diameter horizonti
perpendicularis, diameter gravitatis pendula appellatur.
vitatis centrum acta: Et gravitatis diameter horizonti
perpendicularis, diameter gravitatis pendula appellatur.
DECLARATIO.
Vtin 4æ definitionis figurâ, quævis recta infinita per gravitatis centrum D
acta, corporis A B C diameter gravitatis appellatur: Verum gravitatis diame-
ter ad horizontem recta ut A D gravitatis diameter pendula dicatur.
acta, corporis A B C diameter gravitatis appellatur: Verum gravitatis diame-
ter ad horizontem recta ut A D gravitatis diameter pendula dicatur.
NOTATO.
In priore editione gravitatis diameter definita nobis fuit infinita per gravitatis
ſue centr@ m pendens, ſufficere enim propoſitæ nobis ſcriptioni videbatur. Verum-
eni@@ver@ in ſequenti additamenio ponderoſorũ genera non paulo diligentius
ſue centr@ m pendens, ſufficere enim propoſitæ nobis ſcriptioni videbatur. Verum-
eni@@ver@ in ſequenti additamenio ponderoſorũ genera non paulo diligentius
