1pendicularis, ſcilicet do
nec CG in CD redeat.
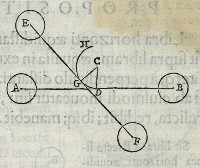
Quando autem CG erit
in CD, linea EF, cùm
ipſi CG ſemper ad rectos
ſit angulos, erit in AB; in
quo ſitu quoq; manebit. li
bra ergo EF in AB hori
zonti æquidiſtantem redi
bit, ibíq; manebit. quod
demonſtrare oportebat.
nec CG in CD redeat.
Quando autem CG erit
in CD, linea EF, cùm
ipſi CG ſemper ad rectos
ſit angulos, erit in AB; in
quo ſitu quoq; manebit. li
bra ergo EF in AB hori
zonti æquidiſtantem redi
bit, ibíq; manebit. quod
demonſtrare oportebat.
4. primi Archi
medis de
æqueponde
rantibus.1. Huius1. Huius.
medis de
æqueponde
rantibus.1. Huius1. Huius.
8[Figure 8]PROPOSITIO III.
Libra horizonti æquidiſtans æqualia in extre
mitatibus, æqualiterq; à perpendiculo diſtan
tia habens pondera, centro infernè collocato, in
hoc ſitu manebit. ſi verò inde moueatur, deor
ſum relicta, ſecundùm partem decliuiorem mo
uebitur.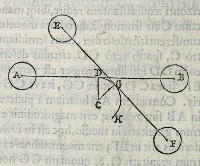
9[Figure 9]
mitatibus, æqualiterq; à perpendiculo diſtan
tia habens pondera, centro infernè collocato, in
hoc ſitu manebit. ſi verò inde moueatur, deor
ſum relicta, ſecundùm partem decliuiorem mo
uebitur.
9[Figure 9]Sit libra AB rectá li
nea horizonti æquidi
ſtans, cuius centrum C
ſit infra libram; perpen
diculumq; ſit CD, quod
horizonti perpendiculare
erit; & diſtantia AD ſit
diſtantiæ DB æqualis;
ſintq; in AB pondera
æqualia, quorum grauita
tis centra ſint in punctis
AB. Dico primùm libram AB in hoc ſitu manere. Quoniam
enim AB bifariam diuiditur à puncto D, & pondera in AB ſunt
æqualia; erit punctum D centrum grauitatis magnitudinis ex
nea horizonti æquidi
ſtans, cuius centrum C
ſit infra libram; perpen
diculumq; ſit CD, quod
horizonti perpendiculare
erit; & diſtantia AD ſit
diſtantiæ DB æqualis;
ſintq; in AB pondera
æqualia, quorum grauita
tis centra ſint in punctis
AB. Dico primùm libram AB in hoc ſitu manere. Quoniam
enim AB bifariam diuiditur à puncto D, & pondera in AB ſunt
æqualia; erit punctum D centrum grauitatis magnitudinis ex