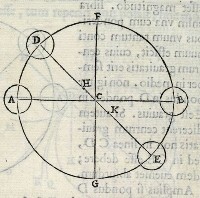
Iiſdem poſitis, duca
tur FCG ipſi AB, &
horizonti perpendicula
ris; & centro C, ſpatio
què CA, circulus deſcri
batur ADFBEG. erunt
puncta ADBE in circu
li circumferentia; cum li
bræ brachia ſint æqualia.
& quoniam in vnam con
ueniunt ſententiam, aſſe
rentes ſcilicet libram DE
neq; in FG moueri, ne
que in DE manere, ſed in AB horizonti æquidiſtantem rediré.
hanc eorum ſententiam nullo modo conſiſtere poſſe oſtendam.
Non enim, ſed ſi quod aiunt, euenerit, vel ideo erit, quia pondus
D pondere E grauius fuerit, vel ſi pondera ſunt æqualia, diſtantiæ,
quibus ſunt poſita, non erunt æquales, hoc eſt CD ipſi CE non erit
æqualis, ſed maior. Quòd autem pondera in DE ſint æqualia, &
diſtantia CD ſit æqualis diſtantiæ CE: hæc ex ſuppoſitione pa
tent. Sed quoniam dicunt pondus in D in eo ſitu pondere in E
grauius eſſe in altero ſitu deorſum: dum pondera ſunt in DE, pun
ctum C non erit amplius centrum grauitatis, nam non manent, ſi
ex C ſuſpendantur; ſed erit in linea CD, ex tertia primi Archi
medis de æqueponderantibus. non autem erit in linea CE, cum pon
dus D grauius ſit pondere E. ſit igitur in H, in quo ſi ſuſpendan
tur, manebunt. Quoniam autem centrum grauitatis ponderum
in AB connexorum eſt punctum C; ponderum verò in DE eſt
punctum H: dum igitur pondera AB mouentur in DE, centrum
grauitatis C verſus D mouebitur, & ad D propius accedet; quod
eſt impoſsibile: cum pondera eandem inter ſe ſe ſeruent diſtantiam.
Vniuſcuiuſq; enim corporis centrum grauitatis in eodem ſemper
eſt ſitu reſpectu ſui corporis. & quamquam punctum C ſit duo
rum corporum AB centrum grauitatis, quia tamen inter ſe ſe ita à
libra connexa ſunt, vt ſemper eodem modo ſe ſe habeant; Ideo
punctum C ita eorum erit centrum grauitatis, ac ſi vna tantum
tur FCG ipſi AB, &
horizonti perpendicula
ris; & centro C, ſpatio
què CA, circulus deſcri
batur ADFBEG. erunt
puncta ADBE in circu
li circumferentia; cum li
bræ brachia ſint æqualia.
& quoniam in vnam con
ueniunt ſententiam, aſſe
rentes ſcilicet libram DE
neq; in FG moueri, ne
que in DE manere, ſed in AB horizonti æquidiſtantem rediré.
hanc eorum ſententiam nullo modo conſiſtere poſſe oſtendam.
Non enim, ſed ſi quod aiunt, euenerit, vel ideo erit, quia pondus
D pondere E grauius fuerit, vel ſi pondera ſunt æqualia, diſtantiæ,
quibus ſunt poſita, non erunt æquales, hoc eſt CD ipſi CE non erit
æqualis, ſed maior. Quòd autem pondera in DE ſint æqualia, &
diſtantia CD ſit æqualis diſtantiæ CE: hæc ex ſuppoſitione pa
tent. Sed quoniam dicunt pondus in D in eo ſitu pondere in E
grauius eſſe in altero ſitu deorſum: dum pondera ſunt in DE, pun
ctum C non erit amplius centrum grauitatis, nam non manent, ſi
ex C ſuſpendantur; ſed erit in linea CD, ex tertia primi Archi
medis de æqueponderantibus. non autem erit in linea CE, cum pon
dus D grauius ſit pondere E. ſit igitur in H, in quo ſi ſuſpendan
tur, manebunt. Quoniam autem centrum grauitatis ponderum
in AB connexorum eſt punctum C; ponderum verò in DE eſt
punctum H: dum igitur pondera AB mouentur in DE, centrum
grauitatis C verſus D mouebitur, & ad D propius accedet; quod
eſt impoſsibile: cum pondera eandem inter ſe ſe ſeruent diſtantiam.
Vniuſcuiuſq; enim corporis centrum grauitatis in eodem ſemper
eſt ſitu reſpectu ſui corporis. & quamquam punctum C ſit duo
rum corporum AB centrum grauitatis, quia tamen inter ſe ſe ita à
libra connexa ſunt, vt ſemper eodem modo ſe ſe habeant; Ideo
punctum C ita eorum erit centrum grauitatis, ac ſi vna tantum