1eſſet magnitudo. libra
enim vna cum ponderi
bus vnum tantum conti
nuum efficit, cuius cen
trum grauitatis erit ſem
per in medio. non igitur
pondus in D pondere in
E eſt grauius. Si autem
dicerent centrum graui
tatis non in linea CD,
ſed in CE eſſe debere;
idem eueniet abſurdum.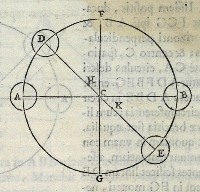 13[Figure 13]
13[Figure 13]
enim vna cum ponderi
bus vnum tantum conti
nuum efficit, cuius cen
trum grauitatis erit ſem
per in medio. non igitur
pondus in D pondere in
E eſt grauius. Si autem
dicerent centrum graui
tatis non in linea CD,
ſed in CE eſſe debere;
idem eueniet abſurdum.
 13[Figure 13]
13[Figure 13]Amplius ſi pondus D
deorſum mouebitur, pondus E ſurſum mouebit. pondus igitur gra
uius, quàm ſit E, in eodemmet ſitu ponderi D æqueponderabit, &
grauia inæqualia æquali diſtantia poſita æqueponderabunt. Adii
ciatur ergo ponderi E aliquod graue, ita vt ipſi D contraponde
ret, ſi ex C ſuſpendantur. ſed cum ſupra oſtenſum ſit punctum C
centrum eſſe grauitatis æqualium ponderum in DE; ſi igitur pon
dus E grauius fuerit pondere D, erit centrum grauitatis in linea
CE. ſitq; hoc centrum K. at per definitionem centri grauitatis, ſi
pondera ſuſpendantur ex K, manebunt. ergo ſi ſuſpendantur ex
C, non manebunt, quod eſt contra hypoteſim: ſed pondus E deor
ſum mouebitur. quòd ſi ex C quoque ſuſpenſa æqueponderarent;
vnius magnitudinis duo eſſent centra grauitatis; quod eſt impoſsi
bile. Non igitur pondus in E grauius eo, quod eſt in D, ipſi D æque
ponderabit, cum ex puncto C fiat ſuſpenſio. Pondera ergo in DE
æqualia ex eorum grauitatis centro C ſuſpenſa, æqueponderabunt,
manebuntquè. quod demonſtrare fuerat propoſitum.
deorſum mouebitur, pondus E ſurſum mouebit. pondus igitur gra
uius, quàm ſit E, in eodemmet ſitu ponderi D æqueponderabit, &
grauia inæqualia æquali diſtantia poſita æqueponderabunt. Adii
ciatur ergo ponderi E aliquod graue, ita vt ipſi D contraponde
ret, ſi ex C ſuſpendantur. ſed cum ſupra oſtenſum ſit punctum C
centrum eſſe grauitatis æqualium ponderum in DE; ſi igitur pon
dus E grauius fuerit pondere D, erit centrum grauitatis in linea
CE. ſitq; hoc centrum K. at per definitionem centri grauitatis, ſi
pondera ſuſpendantur ex K, manebunt. ergo ſi ſuſpendantur ex
C, non manebunt, quod eſt contra hypoteſim: ſed pondus E deor
ſum mouebitur. quòd ſi ex C quoque ſuſpenſa æqueponderarent;
vnius magnitudinis duo eſſent centra grauitatis; quod eſt impoſsi
bile. Non igitur pondus in E grauius eo, quod eſt in D, ipſi D æque
ponderabit, cum ex puncto C fiat ſuſpenſio. Pondera ergo in DE
æqualia ex eorum grauitatis centro C ſuſpenſa, æqueponderabunt,
manebuntquè. quod demonſtrare fuerat propoſitum.
Iordanus de Ponderibus. Hyerommus Cardanus de ſubtilitate. Nicolaus Tartalea de quæſitis, ac inuentionibus. 2. Sup. huius. Ex 4. primi Archim de Aequep.Ex 3. primi Archim de Aequep.1. Suppoſ. huius.
Huic autem poſtremo inconuenienti occurrunt dicentes, im
poſsibile eſſe addere ipſi E pondus adeo minimum, quin adhuc ſi
ex C ſuſpendantur, pondus E ſemper deorſum verſus G moueatur.
quod nos fieri poſſe ſuppoſuimus, atque fieri poſſe credebamus. ex
ceſſum enim ponderis D ſupra pondus E, cum quantitatis ratio
nem habeat, non ſolum minimum eſſe, verum in infinitum diuidi
poſſe immaginabamur, quod quidem ipſi, non ſolum minimum,
poſsibile eſſe addere ipſi E pondus adeo minimum, quin adhuc ſi
ex C ſuſpendantur, pondus E ſemper deorſum verſus G moueatur.
quod nos fieri poſſe ſuppoſuimus, atque fieri poſſe credebamus. ex
ceſſum enim ponderis D ſupra pondus E, cum quantitatis ratio
nem habeat, non ſolum minimum eſſe, verum in infinitum diuidi
poſſe immaginabamur, quod quidem ipſi, non ſolum minimum,
