Rationes tamen af
ferunt, quibus demon
ſtrare nituntur, libram
DE in AB horizon
ti æquidiſtantem ex
neceſsitate redire. Pri
mum quidem oſten
dunt, idem pondus
grauius eſſe in A,
quàm in alio ſitu, quem
æqualitatis ſitum no
minant, cum linea
AB ſit horizonti æ
 17[Figure 17]
17[Figure 17]
quidiſtans. deinde quò propius eſt ipſi A, quouis alio remotiori
grauius eſſe. Vt pondus in A grauius eſſe, quàm in D; & in D,
quàm in L. ſimiliter in A grauius, quam in N; & in N grauius,
quàm in M. Vnum tantùm conſiderando pondus in altero libræ
brachio ſurſum deorſumq; moto. Quia (inquiunt) poſita trutina
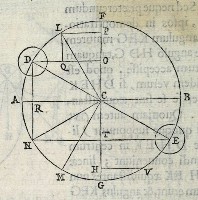
in CF, pondus in A longius eſt à trutina, quàm in D: & in D
longius, quàm in L. ductis enim DO LP ipſi CF perpendicula
ribus, linea AC maior eſt, quàm DO, & DO ipſa LP. quod
idem euenit in punctis NM. deinde ex quo loco (aiunt) pon
dus velocius mouetur, ibi grauius eſt; velocius autem ex A, quàm
ab alio ſitu mouetur; ergo in A grauius eſt. ſimili modo, quò
propius eſt ipſi A, velocius quoque mouetur; ergo in D gra
uius erit, quàm in L. Altera deinde cauſa, quam ex rectiori, & obli
quiori motu deducunt, eſt; quò pondus in arcubus æqualibus re
ctius deſcendit, grauius eſſe videtur; cum pondus liberum, atq;
ſolutum ſuaptè natura rectè moueatur; ſed in A rectius deſcen
dit; ergo in A grauius erit. hocq; oſtendunt accipiendo arcum
AN arcui LD æqualem; à punctiſq; NL lineæ FG (quam
etiam directionis vocant) æquidiſtantes ducantur NRLQ, quæ
lineas AB DO ſecent in QR; & à puncto N ipſi FG perpen
dicularis ducatur NT. rectèq; demonſtrant LQ ipſi PO æqua
lem eſſe, & NR ipſi CT; lineamq; NR ipſa LQ maiorem eſſe.
Quoniam autem deſcenſu; ponderis ex A vſq; ad N per circum
ferunt, quibus demon
ſtrare nituntur, libram
DE in AB horizon
ti æquidiſtantem ex
neceſsitate redire. Pri
mum quidem oſten
dunt, idem pondus
grauius eſſe in A,
quàm in alio ſitu, quem
æqualitatis ſitum no
minant, cum linea
AB ſit horizonti æ
 17[Figure 17]
17[Figure 17]quidiſtans. deinde quò propius eſt ipſi A, quouis alio remotiori
grauius eſſe. Vt pondus in A grauius eſſe, quàm in D; & in D,
quàm in L. ſimiliter in A grauius, quam in N; & in N grauius,
quàm in M. Vnum tantùm conſiderando pondus in altero libræ
brachio ſurſum deorſumq; moto. Quia (inquiunt) poſita trutina
in CF, pondus in A longius eſt à trutina, quàm in D: & in D
longius, quàm in L. ductis enim DO LP ipſi CF perpendicula
ribus, linea AC maior eſt, quàm DO, & DO ipſa LP. quod
idem euenit in punctis NM. deinde ex quo loco (aiunt) pon
dus velocius mouetur, ibi grauius eſt; velocius autem ex A, quàm
ab alio ſitu mouetur; ergo in A grauius eſt. ſimili modo, quò
propius eſt ipſi A, velocius quoque mouetur; ergo in D gra
uius erit, quàm in L. Altera deinde cauſa, quam ex rectiori, & obli
quiori motu deducunt, eſt; quò pondus in arcubus æqualibus re
ctius deſcendit, grauius eſſe videtur; cum pondus liberum, atq;
ſolutum ſuaptè natura rectè moueatur; ſed in A rectius deſcen
dit; ergo in A grauius erit. hocq; oſtendunt accipiendo arcum
AN arcui LD æqualem; à punctiſq; NL lineæ FG (quam
etiam directionis vocant) æquidiſtantes ducantur NRLQ, quæ
lineas AB DO ſecent in QR; & à puncto N ipſi FG perpen
dicularis ducatur NT. rectèq; demonſtrant LQ ipſi PO æqua
lem eſſe, & NR ipſi CT; lineamq; NR ipſa LQ maiorem eſſe.
Quoniam autem deſcenſu; ponderis ex A vſq; ad N per circum
