18tibus omninò naturalibus) de ipſa ſermo haberi poſsit: ſine qui
bus eorum, quæ libræ accidunt, veræ caulæ reperiri nullo mo
do poſsint.
bus eorum, quæ libræ accidunt, veræ caulæ reperiri nullo mo
do poſsint.
Præterea ſi adhuc ſup
poſitionem conceda
mus; à conſideratione
libræ longè recedunt;
dum eo pacto, vt libra
DE in AB redire de
beat, diſcurrunt. ſemper
enim alterum pondus
ſeorſum accipiunt, putá
D, vel E; ac ſi modò vnum
modò alterum in libra
conſtitutum eſſet, nec
vllo modo ambo con
 34[Figure 34]
34[Figure 34]
nexa; cuius tamen oppoſitum omninò fieri oportet; neq; alterum
ſine altero rectè conſiderari poteſt; cùm de ipſis in libra conſti
tutis ſermo habeatur. cùm enim dicunt, deſcenſum ponderis in
D minus obliquum eſſe deſcenſu ponderis in E; erit pondus in
D per ſuppoſitionem grauius pondere in E: quare cùm ſit graui
us, neceſſe eſt deorſum moueri, libramq; DE in AB redire: di
ſcurſus iſte nullius prorſus momenti eſt. Primùm quidem ſem
per argumentantur, ac ſi pondera in DE deſcendere debeant,
vnius tantùm ſine alterius connexione conſiderando deſcenſum.
poſtremò tamen ob ponderum deſcenſuum comparationem colli
gentes inferunt, pondus in D deorſum moueri, & pondus in E
ſurſum, vtraq; ſimul in libra inuicem connexa accipientes. ve
rùm ex iiſdemmet, quibus vtuntur, principiis, ac demonſtratio
nibus, oppoſitum eius, quod defendere conantur, facillimè col
ligi poteſt. Nam ſi comparetur deſcenſus ponderis in D cum a
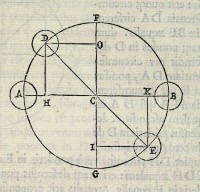
ſcenſu ponderis in E, vt ductis EK DH ipſi AB perpendicula
ribus; cùm angulus DCH ſit æqualis angulo ECk; & angulus
DHC rectus æqualis eſt recto E k C; & latus DC lateri CE æqua
le: erit triangulum CDH triangulo CEk æquale, & latus DH la
poſitionem conceda
mus; à conſideratione
libræ longè recedunt;
dum eo pacto, vt libra
DE in AB redire de
beat, diſcurrunt. ſemper
enim alterum pondus
ſeorſum accipiunt, putá
D, vel E; ac ſi modò vnum
modò alterum in libra
conſtitutum eſſet, nec
vllo modo ambo con
 34[Figure 34]
34[Figure 34]nexa; cuius tamen oppoſitum omninò fieri oportet; neq; alterum
ſine altero rectè conſiderari poteſt; cùm de ipſis in libra conſti
tutis ſermo habeatur. cùm enim dicunt, deſcenſum ponderis in
D minus obliquum eſſe deſcenſu ponderis in E; erit pondus in
D per ſuppoſitionem grauius pondere in E: quare cùm ſit graui
us, neceſſe eſt deorſum moueri, libramq; DE in AB redire: di
ſcurſus iſte nullius prorſus momenti eſt. Primùm quidem ſem
per argumentantur, ac ſi pondera in DE deſcendere debeant,
vnius tantùm ſine alterius connexione conſiderando deſcenſum.
poſtremò tamen ob ponderum deſcenſuum comparationem colli
gentes inferunt, pondus in D deorſum moueri, & pondus in E
ſurſum, vtraq; ſimul in libra inuicem connexa accipientes. ve
rùm ex iiſdemmet, quibus vtuntur, principiis, ac demonſtratio
nibus, oppoſitum eius, quod defendere conantur, facillimè col
ligi poteſt. Nam ſi comparetur deſcenſus ponderis in D cum a
ſcenſu ponderis in E, vt ductis EK DH ipſi AB perpendicula
ribus; cùm angulus DCH ſit æqualis angulo ECk; & angulus
DHC rectus æqualis eſt recto E k C; & latus DC lateri CE æqua
le: erit triangulum CDH triangulo CEk æquale, & latus DH la
