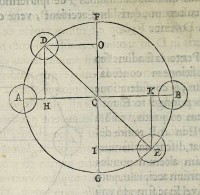
1teri Ek æquale. cùm
autem angulus DCA
ſit angulo ECB æqua
lis: erit quoq; circum
ferentia DA circumferen
tiæ BE æqualis. dum
itaq; pondus in D de
ſcendit per circumfe
rentiam DA, pondus
in E per circumferen
tiam EB ipſi DA æ
qualem aſcendit. & de
ſcenſus ponderis in D de
directo (more ipſorum)
 35[Figure 35]
35[Figure 35]
capiet DH; aſcenſus verò ponderis in E de directo capiet Ek ip
ſi DH æqualem: erit itaq; deſcenſus ponderis in D aſcenſui pon
deris in E æqualis, & qualis erit propenſio vnius ad motum deor
sum, talis etiam erit reſiſtentia alterius ad motum ſurſum. re
ſiſtentia ſcilicet violentiæ ponderis in E in aſcenſu naturali po
tentiæ ponderis in D in deſcenſu contrà nitendo apponitur; cùm
ſit ipſi æqualis. quò enim pondus in D naturali potentia deor
ſum velocius deſcendit, eò tardius pondus in E violenter aſcendit.
quare neutrum ipſorum alteri præponderabit, cùm ab æquali non
proueniat actio. Non igitur pondus in D pondus in E ſurſum
mouebit. ſi enim moueret; neceſſe eſſet, pondus in D maiorem
habere virtutem deſcendendo, quàm pondus in E aſcendendo;
ſed hæc ſunt æqualia: ergo pondera manebunt. & grauitas pon
deris in D grauitati ponderis in E æqualis erit. Præterea quoniam
ſupponunt, quò pondus à linea directionis FG magis diſtat, eò
grauius eſſe: Idcirco ductis quoq; à punctis DE ipſi FG perpen
dicularibus DO EI; ſimili modo demonſtrabitur, triangulum
CDO triangulo CEI æqualem eſſe: & lineam DO ipſi EI æqua
lem. tam igitur diſtat à linea FG pondus in D, quàm pondus in
E. ex ipſorum igitur rationibus, atq; ſuppoſitionibus, pondera
in DE æquè grauia erunt. Amplius quid prohibet, quin libram
DE ex neceſsitate in FG moueri ſimili ratione oſtendatur? Pri
autem angulus DCA
ſit angulo ECB æqua
lis: erit quoq; circum
ferentia DA circumferen
tiæ BE æqualis. dum
itaq; pondus in D de
ſcendit per circumfe
rentiam DA, pondus
in E per circumferen
tiam EB ipſi DA æ
qualem aſcendit. & de
ſcenſus ponderis in D de
directo (more ipſorum)
 35[Figure 35]
35[Figure 35]capiet DH; aſcenſus verò ponderis in E de directo capiet Ek ip
ſi DH æqualem: erit itaq; deſcenſus ponderis in D aſcenſui pon
deris in E æqualis, & qualis erit propenſio vnius ad motum deor
sum, talis etiam erit reſiſtentia alterius ad motum ſurſum. re
ſiſtentia ſcilicet violentiæ ponderis in E in aſcenſu naturali po
tentiæ ponderis in D in deſcenſu contrà nitendo apponitur; cùm
ſit ipſi æqualis. quò enim pondus in D naturali potentia deor
ſum velocius deſcendit, eò tardius pondus in E violenter aſcendit.
quare neutrum ipſorum alteri præponderabit, cùm ab æquali non
proueniat actio. Non igitur pondus in D pondus in E ſurſum
mouebit. ſi enim moueret; neceſſe eſſet, pondus in D maiorem
habere virtutem deſcendendo, quàm pondus in E aſcendendo;
ſed hæc ſunt æqualia: ergo pondera manebunt. & grauitas pon
deris in D grauitati ponderis in E æqualis erit. Præterea quoniam
ſupponunt, quò pondus à linea directionis FG magis diſtat, eò
grauius eſſe: Idcirco ductis quoq; à punctis DE ipſi FG perpen
dicularibus DO EI; ſimili modo demonſtrabitur, triangulum
CDO triangulo CEI æqualem eſſe: & lineam DO ipſi EI æqua
lem. tam igitur diſtat à linea FG pondus in D, quàm pondus in
E. ex ipſorum igitur rationibus, atq; ſuppoſitionibus, pondera
in DE æquè grauia erunt. Amplius quid prohibet, quin libram
DE ex neceſsitate in FG moueri ſimili ratione oſtendatur? Pri
