10290IO. BAPT. BENED.
mæ iam dictæ in maiorem eorum, hoc eſt quod fit ex quinque in .3. quod erit .15.
Vt
autem medium terminum harmonicum inter iſtos habeamus, accipiatur duplum pro-
ducti, quod fit ex primis minimis terminis, quod erit .12.
autem medium terminum harmonicum inter iſtos habeamus, accipiatur duplum pro-
ducti, quod fit ex primis minimis terminis, quod erit .12.
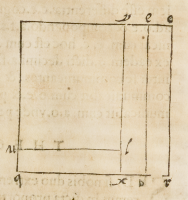
Cuius rei ſpeculatio eſt iſta:
ſignificentur duo termini datæ proportionis ab .q.b.
et .b.r. quorum ſumma erit .q.r. cuius quadratum ſit .q.o. ſit etiam imaginata .b.e.
parallela ad .o.r. Sitque; .b.x. æqualis .b.r. et .q.u. ſimiliter, & ducatur .x.y. parallela ad
r.o. et .u.l. ad .q.x. Tunc habebimus .b.o. æquale ei producto, quod fit ex .q.r. in .b.r.
et .b.y. eidem etiam æquale, et .q.e. pro producto, quod fit ex .q.r. in .q.b. et .q.l. pro
eo, quod fit ex .q.x. in .b.r. Vnde .q.l. cum .b.y. æquale fiet duplo ei, quod fit ex .q.b.
in .b.r. Dico nunc .b.o. eſſe minimum terminum eorum, quos quærimus, et .y.b. cum .
x.u. medium .q.e. verò maximum huiuſmodi proportionalitatis.
et .b.r. quorum ſumma erit .q.r. cuius quadratum ſit .q.o. ſit etiam imaginata .b.e.
parallela ad .o.r. Sitque; .b.x. æqualis .b.r. et .q.u. ſimiliter, & ducatur .x.y. parallela ad
r.o. et .u.l. ad .q.x. Tunc habebimus .b.o. æquale ei producto, quod fit ex .q.r. in .b.r.
et .b.y. eidem etiam æquale, et .q.e. pro producto, quod fit ex .q.r. in .q.b. et .q.l. pro
eo, quod fit ex .q.x. in .b.r. Vnde .q.l. cum .b.y. æquale fiet duplo ei, quod fit ex .q.b.
in .b.r. Dico nunc .b.o. eſſe minimum terminum eorum, quos quærimus, et .y.b. cum .
x.u. medium .q.e. verò maximum huiuſmodi proportionalitatis.
Primum ergo certi ſcimus ex prima ſexti vel .18. ſeptimi eandem exiſtere pro-
portionem .q.e. ad .b.o. ſeu ad .b.y. quæ .q.b. ad .b.r: ſed .u.y. ad .u.x. eſt vt .y.l. ad .l.x.
hoc eſt vt .q.b. ad .b.r. ideſt vt .q.e. ad .b.o. & ſumma .u.y. cum .u.x. ideſt .q.y. minor eſt
quam .q.e. maximus terminus per .b.y. minimum ter-
minum. & coniunctim .q.y. ad .q.l. vt .y.x. ad .x.l. hoc eſt
 140[Figure 140]
vt .q.r. ad .r.b.
Vnde ex ſpeculatione præcedentis theo
140[Figure 140]
vt .q.r. ad .r.b.
Vnde ex ſpeculatione præcedentis theo
rematis, ſequitur .u.y. eſſe differentiam inter maximum
& medium terminum, et .u.x. eſſe differentiam inter
medium & minimum dictæ proportionalitatis. Nam
eadem proportio eſt .q.e. maximi termini ad .b.o. mi-
nimi. quæ .u.y. (differentia inter .q.e. & gnomonem .
u.b.y.) ad .u.x. (differentia inter dictum .u.b.y. et .b.y.
minimum terminum, quia ſunt ambæ ut .q.b. ad .b.r.
vt diximus. Quare .b.y. coniunctum cum .x.u. medius
terminus erit, qui quidem (vt dictum eſt) duplus eſt ei
quod fit ex .q.b. in .b.r.
portionem .q.e. ad .b.o. ſeu ad .b.y. quæ .q.b. ad .b.r: ſed .u.y. ad .u.x. eſt vt .y.l. ad .l.x.
hoc eſt vt .q.b. ad .b.r. ideſt vt .q.e. ad .b.o. & ſumma .u.y. cum .u.x. ideſt .q.y. minor eſt
quam .q.e. maximus terminus per .b.y. minimum ter-
minum. & coniunctim .q.y. ad .q.l. vt .y.x. ad .x.l. hoc eſt
rematis, ſequitur .u.y. eſſe differentiam inter maximum
& medium terminum, et .u.x. eſſe differentiam inter
medium & minimum dictæ proportionalitatis. Nam
eadem proportio eſt .q.e. maximi termini ad .b.o. mi-
nimi. quæ .u.y. (differentia inter .q.e. & gnomonem .
u.b.y.) ad .u.x. (differentia inter dictum .u.b.y. et .b.y.
minimum terminum, quia ſunt ambæ ut .q.b. ad .b.r.
vt diximus. Quare .b.y. coniunctum cum .x.u. medius
terminus erit, qui quidem (vt dictum eſt) duplus eſt ei
quod fit ex .q.b. in .b.r.
THEOREMA CXXXV.
ALIVM etiam modum ab antiquis traditum ad hoc problema perficiendum
inueni, qui talis eſt. Inueniatur primo inter datos terminos extremos, me-
dius terminus in arithmetica proportione, per quem
 141[Figure 141]
multiplicetur vnuſquiſque dictorum extremorum,
141[Figure 141]
multiplicetur vnuſquiſque dictorum extremorum,
deinde multiplicentur ipſi extremi interſe, vnde
habebimus tria producta eadem proportione inui
cem exiſtentia, vt quærebatur.
inueni, qui talis eſt. Inueniatur primo inter datos terminos extremos, me-
dius terminus in arithmetica proportione, per quem
deinde multiplicentur ipſi extremi interſe, vnde
habebimus tria producta eadem proportione inui
cem exiſtentia, vt quærebatur.
Exempli gratia, ponamus duos propoſitos ter-
minos eſſe .3. et .2. quorum medius arithmeticè
eſſet .2. cum dimidia vnitate, per quem cum vnum
quemque priorum multiplicauerimus, emergent no-
bis duo producta, quorum primum ideſt maius eſſet
7. cum dimidia vnitate, reliquum verò eſſet
quinque, productum poſteà quod ex ipſis extremis
prouenit, erit .6. quod quidem eſt harmonicè collo
catum inter .7. cum dimidia vnitate, & quinque.
minos eſſe .3. et .2. quorum medius arithmeticè
eſſet .2. cum dimidia vnitate, per quem cum vnum
quemque priorum multiplicauerimus, emergent no-
bis duo producta, quorum primum ideſt maius eſſet
7. cum dimidia vnitate, reliquum verò eſſet
quinque, productum poſteà quod ex ipſis extremis
prouenit, erit .6. quod quidem eſt harmonicè collo
catum inter .7. cum dimidia vnitate, & quinque.
Cuius rei ſpeculatio omnis à præcedenti theore-
mate dependet. Sint exempli gratia, duo termini
mate dependet. Sint exempli gratia, duo termini
