118106IO. BAPT. BENED.
SEDijdem errores proueniunt exſummis partium ſimplicium.
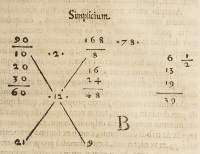
Vtexempli gratia, in figura .B. ſumma propoſita partium ſimplicium eſt .39.
vt diximus, eo quòd ab ipſo .50. detraxerimus .11. ſumma ſcilicet numerorum adij
ciendorum ad efficiendas partes compofitas, ſumma poſteà fimplicium partium
primæ poſitionis, erit .60. eo quòd prima pars erat .10. ſecunda autem ſimplex 20.
tertia verò fimplex .30. iuxta ordinem propoſiti. Summa deinde ſimplicium partium
fecundæ poſitionis effet .48. quia prima eius pars erat .8. ſecunda verò ſimplex .16.
tertia autem ſimplex .24. vnde prima ſumma excederet datam .39. per .21. differen-
tiæ, ſecunda verò per .9. vt ſupra vidimus de ſummis compoſitis à dato .50. compo-
fito, & hoc quidem mirandum non eft, quod ſcilicet tres ſummæ fimplicium par-
tium ſintinuicem inæqua-
les, ijſdem differentijs me-
 162[Figure 162]Simpricium
diantibus, quibus differunt
162[Figure 162]Simpricium
diantibus, quibus differunt
dictæ tres ſummæ compofi
tæ, cum ab vnaquaque con
poſitarum ablatus fit nume-
rus .11. æqualiter, vnde ex
neceſſitate, permutando,
earum differentiæ relinquem
dæ erant æquales inuicem
ex .78. theoremate hu-
ius noſtri lib. ſummæ enim
compofitæ erant .71. 59. et
50. fimplices verò .60. 48.
et .39. differentes à primis
per .11. vt dictum eft, qua
re veritas ita manabit à compofitis, quemadmodum à fimplicibus, ſed à fimplici-
bus per ſe, & a compofitis per accidens vtiam iam videbimus.
vt diximus, eo quòd ab ipſo .50. detraxerimus .11. ſumma ſcilicet numerorum adij
ciendorum ad efficiendas partes compofitas, ſumma poſteà fimplicium partium
primæ poſitionis, erit .60. eo quòd prima pars erat .10. ſecunda autem ſimplex 20.
tertia verò fimplex .30. iuxta ordinem propoſiti. Summa deinde ſimplicium partium
fecundæ poſitionis effet .48. quia prima eius pars erat .8. ſecunda verò ſimplex .16.
tertia autem ſimplex .24. vnde prima ſumma excederet datam .39. per .21. differen-
tiæ, ſecunda verò per .9. vt ſupra vidimus de ſummis compoſitis à dato .50. compo-
fito, & hoc quidem mirandum non eft, quod ſcilicet tres ſummæ fimplicium par-
tium ſintinuicem inæqua-
les, ijſdem differentijs me-
dictæ tres ſummæ compofi
tæ, cum ab vnaquaque con
poſitarum ablatus fit nume-
rus .11. æqualiter, vnde ex
neceſſitate, permutando,
earum differentiæ relinquem
dæ erant æquales inuicem
ex .78. theoremate hu-
ius noſtri lib. ſummæ enim
compofitæ erant .71. 59. et
50. fimplices verò .60. 48.
et .39. differentes à primis
per .11. vt dictum eft, qua
re veritas ita manabit à compofitis, quemadmodum à fimplicibus, ſed à fimplici-
bus per ſe, & a compofitis per accidens vtiam iam videbimus.
ANtiquorumigitur primus m odus vtitur regula detribus, hocordine, multi-
plicando ſcilicet ſecundum errorem, qui eft .9. cum differentia primarum par
tium pofitarum, quæ eft .2. & productum diuidendo per differentiam errorum, quæ
eft .12. proueniens poftea quod eft .1. cum dimidio additur hoc loco primæ parti ſe-
cundæ poſitionis. &&c.. quòd benè ſe habet. Vbi animaduertendum eſt, quod ille
numerus .12. non eft accipiendus per ſe vt differentia errorum hoc eft .21. et .9. nifi
peràccidens, fed benè perfe, vt differentia inter .60. er .48. ſimplices ſummas, quem
admodum .9. in hoc propoſito eft differentia per ſe inter .48. et .39 per accidens ve-
ro inter .59. et .50.
plicando ſcilicet ſecundum errorem, qui eft .9. cum differentia primarum par
tium pofitarum, quæ eft .2. & productum diuidendo per differentiam errorum, quæ
eft .12. proueniens poftea quod eft .1. cum dimidio additur hoc loco primæ parti ſe-
cundæ poſitionis. &&c.. quòd benè ſe habet. Vbi animaduertendum eſt, quod ille
numerus .12. non eft accipiendus per ſe vt differentia errorum hoc eft .21. et .9. nifi
peràccidens, fed benè perfe, vt differentia inter .60. er .48. ſimplices ſummas, quem
admodum .9. in hoc propoſito eft differentia per ſe inter .48. et .39 per accidens ve-
ro inter .59. et .50.
Cognoſcendum igitur eft mediante .24. quinti Eucli. quod eadem proportio
eft primæ ſummæ (ſimplicium dico) ad ſuam primam partem, quæ ſecundæ ſum-
mæ ad ſuam, & tertiæ ſummæ ad fuam fimiliter (vbi rectè etiam feciffent hoc in lo-
co antiqui ſi multiplicauiffent tertiam ſummam fim plicem cum prima parte prioris
fummæ fimplicis, & productum diuififfent per primam ſummam, vnde prima pars
quæſita tertiæ ſummæ orta fuiffet, abſque ullo negotio ipfius plus velminus) Quare
habebimus tres terminos antecedentes ab vna parte, & tres terminos conſequen-
tesab alia parte continentes vnam eandemque; proportionem, vnde ex .19. quinti,
vel .12. ſeptimi eorum differentiæ proportionales erunt, hoc eft, quod eadem propor
eft primæ ſummæ (ſimplicium dico) ad ſuam primam partem, quæ ſecundæ ſum-
mæ ad ſuam, & tertiæ ſummæ ad fuam fimiliter (vbi rectè etiam feciffent hoc in lo-
co antiqui ſi multiplicauiffent tertiam ſummam fim plicem cum prima parte prioris
fummæ fimplicis, & productum diuififfent per primam ſummam, vnde prima pars
quæſita tertiæ ſummæ orta fuiffet, abſque ullo negotio ipfius plus velminus) Quare
habebimus tres terminos antecedentes ab vna parte, & tres terminos conſequen-
tesab alia parte continentes vnam eandemque; proportionem, vnde ex .19. quinti,
vel .12. ſeptimi eorum differentiæ proportionales erunt, hoc eft, quod eadem propor
