Commandino, Federico - Liber de centro gravitatis solidorum

Commandino, Federico, Liber de centro gravitatis solidorum, 1565

Table of figures

[Figure 11]

[Figure 12]

[Figure 13]

[Figure 14]

[Figure 15]

[Figure 16]

[Figure 17]

[Figure 18]

[Figure 19]

[Figure 20]

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

1cta bd in g puncto, ducatur cg; & protrahatur ad circuli
uſque circumferentiam; quæ ſecet ae in h. Similiter conclu
demus cg per centrum circuli tranſire: & bifariam ſecate
lineam ae; itemque; lineas bd, ae inter ſe æquidiſtantes eſſe.
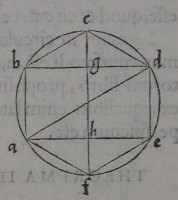
Cum igitur cg per centrum circuli tranſeat; & ad punctum
f perueniat neceſſe eſt: quòd cdef ſit dimidium circumfe

5[Figure 5]

rentiæ circuli. Quare in eadem
diametro cf erunt centra gra
uitatis triangulorum bcd,
afe, & quadrilateri abde, ex
quibus conſtat hexagonum ab
cdef. perſpicuum eſt igitur in
ipſa cf eſſe circuli centrum, &
centrum grauitatis hexagoni.
Rurſus ducta altera diametro
ad, eiſdem rationibus oſtende
mus in ipſa utrumque centrum
ineſſe. Centrum ergo grauita
tis hexagoni, & centrum circuli idem erit.

13 Archi
medis.
9. eiusdem
m

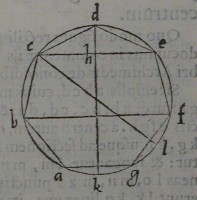
Sit heptagonum abcdefg æquilaterum atque æquian

6[Figure 6]
gulum in circulo deſcriptum:
& iungantur ce, bf, ag: di
uiſa autem ce bifariam in pun
cto h: & iuncta dh produca
tur in k. non aliter demon
ſtrabimus in linea dk eſſe cen
trum circuli, & centrum gra
uitatis trianguli cde, & tra
peziorum bcef, abfg, hoc
eſt centrum totius heptago
ni: & rurſus eadem centra in
alia diametro cl ſimiliter du
cta contineri. Quare & centrum grauitatis heptagoni, &
centrum circuli in idem punctum conueniunt. Eodem

Text layer

Text normalization

Search