13
PRONVNCIATA CEN-
TVM, CVM INTER PRETATIONIBVS, V-
TILITATIBVS, ET EXEMPLIS EORVNDEM APER-
tiſsimis, ſuper inſtrumento nouo Primi Mobilis, recens iam à Petro
Apiano cõpoſita & conſcripta, magno futura uſui omnibus Aſtro
nomiæ ſtudioſis, fœliciter hic incipiunt.
TVM, CVM INTER PRETATIONIBVS, V-
TILITATIBVS, ET EXEMPLIS EORVNDEM APER-
tiſsimis, ſuper inſtrumento nouo Primi Mobilis, recens iam à Petro
Apiano cõpoſita & conſcripta, magno futura uſui omnibus Aſtro
nomiæ ſtudioſis, fœliciter hic incipiunt.
PRincipio cõpoſiturus inſtrumentũ, quo omne illud, q̊dcũ in uniuerſo pri
mo Mobili inquiri poteſt, inueniatur, Duc lineã rectam ea longitudine, q̃
magnitudini ſiue quãtitati ꝓpoſiti inſtrumenti reſpondeat, Ad huius lineæ
finẽ ſeu extremitatẽ dextri lateris pone A, ex altera parte B. Deinde ex A
lineã erige perpendicularẽ, eadem longitudine plano´ æquali lineæ A B,
& in altera extremitate q̃ eminet, ſcribe C. Mox circinũ altero illo pede fixo & immoto
repone in A, mobilẽ aũt pedẽ educ extenſum in C uſ, & ſic circulũ deſcribe à C uſ in
B, at hoc modo habebis ante te deſcriptum iamiam quadrantẽ, quartã. ſ. circuli totius
partẽ ex tribus illis literis A B C. Ad hæc circulũ iſtũ à B in C diuide in 90 partes æqua-
11Quomodo
Quadrans
in 90. par-
tes diuidi
debeat. les, id in hunc modũ. Primũ omniũ in tres partes æquales, deinde quãlibet earũ rurſus
in tres alias ꝑtes æquales, mox ſingulas illas adhuc partire in duas, & has poſtremò in 5.
at ſic circulũ habebis à B uſ in C diuiſum apte in 90. ꝑtes æquales, quas graduũ ap-
pellatione cõtinemus. Et hæc puncta graduũ occultè quidẽ deſcribi debent, ut facile de-
leri poſsint. Cæterũijs ita peractis, porrò adhuc diuide lineã A B in duas ꝑtes in pũcto
D, ſimiliter & lineã A C in pũcto E, circinũ pone in D altero pede fixo, altero exten
ſo deſcribe circulũ ex A uſ in B, circinũ ita immotũ relinque, & pedem alterũ colloca in
E, altero aũt ſimiliter duc ſemicirculũ ab à uſ in C, ita, ut duo illi interſectionẽ mutuã
habeant in pũcto F. At iſti iam ſemicirculi duo illi ſuntueri, qui ad diuiſionem ſinuum
& neceſſario hic requirũtur & adpoſite uſurpantur, q̊d hoc loco præmonuiſſe te oportu
it, nobis´ adeo conſultũ uiſum eſt, eo maxime ut deinceps ſcias ꝗd uelimus, quotieſcũ
de circulis ſinuũ diſſeremus. In pũcto aũt A filum adfigi oportet, quo uſui fit accommo
datior. Deinde punctis D E applica regulã, & pinge aut trahe lineã occultam ex D in E
& eam diuide p mediũ in puncto G, poſthac pone circinũ pede fixo, ſcilicet fixo in G, al-
tero extẽſo in B uel C deſcribe circulũ, & ſic circulũ deſcribe à C uſ in B, ita tamẽ, ut ap
pareat circulus eminere aliquantulũ ultra B & C. Iterũ expande circinũ, & protrahe cir
culũ tantũ ſolummodo diſtantẽ à iam ducto circulo, ꝙ inter ipſos poſsint cadere ſingula
res graduũ diuiſiones. Rurſus iterũ comprime circinũ, & depinge in eodẽ centro tertiũ
circulũ tantũ diſtantem à primo, ut inter ipſos poſsit ſcribi numerus graduũ diſtinctorũ
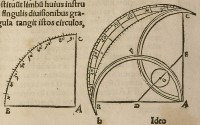 3[Figure 3]
ꝑ 5 &
5.
Hi circuli ſic rite deſcripti, cõſtituũt limbũ huius inſtru
3[Figure 3]
ꝑ 5 &
5.
Hi circuli ſic rite deſcripti, cõſtituũt limbũ huius inſtru
mẽti. Demũ applica regulã cẽtro A & fingulis diuiſionibus gra-
duũ in circulo B C occulto, & ubi regula tangit iſtos circulos,
duc lineas minutas à primo citculo in
ſecũdũ, linea uero à 5. gradu ducenda
erit de ſecũdo circulo in tertiũ. Tandẽ
in ſpacio primi & tertij, incipiẽdo à B
ſcribẽdo uerſus C in primo ſpacio 5.
in ſecũdo 10, in tertio 15, & ſic de alijs
numeris ꝑ ꝗnariũ aſcẽdendo uſ ad
90. q̃ circa C ſedẽ ſibi uendicabunt.
Hactenus de compoſitiõe limbi Qua
drantis, cuius has ſume figuras.
mo Mobili inquiri poteſt, inueniatur, Duc lineã rectam ea longitudine, q̃
magnitudini ſiue quãtitati ꝓpoſiti inſtrumenti reſpondeat, Ad huius lineæ
finẽ ſeu extremitatẽ dextri lateris pone A, ex altera parte B. Deinde ex A
lineã erige perpendicularẽ, eadem longitudine plano´ æquali lineæ A B,
& in altera extremitate q̃ eminet, ſcribe C. Mox circinũ altero illo pede fixo & immoto
repone in A, mobilẽ aũt pedẽ educ extenſum in C uſ, & ſic circulũ deſcribe à C uſ in
B, at hoc modo habebis ante te deſcriptum iamiam quadrantẽ, quartã. ſ. circuli totius
partẽ ex tribus illis literis A B C. Ad hæc circulũ iſtũ à B in C diuide in 90 partes æqua-
11Quomodo
Quadrans
in 90. par-
tes diuidi
debeat. les, id in hunc modũ. Primũ omniũ in tres partes æquales, deinde quãlibet earũ rurſus
in tres alias ꝑtes æquales, mox ſingulas illas adhuc partire in duas, & has poſtremò in 5.
at ſic circulũ habebis à B uſ in C diuiſum apte in 90. ꝑtes æquales, quas graduũ ap-
pellatione cõtinemus. Et hæc puncta graduũ occultè quidẽ deſcribi debent, ut facile de-
leri poſsint. Cæterũijs ita peractis, porrò adhuc diuide lineã A B in duas ꝑtes in pũcto
D, ſimiliter & lineã A C in pũcto E, circinũ pone in D altero pede fixo, altero exten
ſo deſcribe circulũ ex A uſ in B, circinũ ita immotũ relinque, & pedem alterũ colloca in
E, altero aũt ſimiliter duc ſemicirculũ ab à uſ in C, ita, ut duo illi interſectionẽ mutuã
habeant in pũcto F. At iſti iam ſemicirculi duo illi ſuntueri, qui ad diuiſionem ſinuum
& neceſſario hic requirũtur & adpoſite uſurpantur, q̊d hoc loco præmonuiſſe te oportu
it, nobis´ adeo conſultũ uiſum eſt, eo maxime ut deinceps ſcias ꝗd uelimus, quotieſcũ
de circulis ſinuũ diſſeremus. In pũcto aũt A filum adfigi oportet, quo uſui fit accommo
datior. Deinde punctis D E applica regulã, & pinge aut trahe lineã occultam ex D in E
& eam diuide p mediũ in puncto G, poſthac pone circinũ pede fixo, ſcilicet fixo in G, al-
tero extẽſo in B uel C deſcribe circulũ, & ſic circulũ deſcribe à C uſ in B, ita tamẽ, ut ap
pareat circulus eminere aliquantulũ ultra B & C. Iterũ expande circinũ, & protrahe cir
culũ tantũ ſolummodo diſtantẽ à iam ducto circulo, ꝙ inter ipſos poſsint cadere ſingula
res graduũ diuiſiones. Rurſus iterũ comprime circinũ, & depinge in eodẽ centro tertiũ
circulũ tantũ diſtantem à primo, ut inter ipſos poſsit ſcribi numerus graduũ diſtinctorũ
mẽti. Demũ applica regulã cẽtro A & fingulis diuiſionibus gra-
duũ in circulo B C occulto, & ubi regula tangit iſtos circulos,
duc lineas minutas à primo citculo in
ſecũdũ, linea uero à 5. gradu ducenda
erit de ſecũdo circulo in tertiũ. Tandẽ
in ſpacio primi & tertij, incipiẽdo à B
ſcribẽdo uerſus C in primo ſpacio 5.
in ſecũdo 10, in tertio 15, & ſic de alijs
numeris ꝑ ꝗnariũ aſcẽdendo uſ ad
90. q̃ circa C ſedẽ ſibi uendicabunt.
Hactenus de compoſitiõe limbi Qua
drantis, cuius has ſume figuras.
