148136IO. BAPT. BENED.
cere oportet.
Ratio verò ab ipſo adducta propter quam .E. repreſentatur oculo al-
tius quam .b. nempe eo quod .A. ſuperſtet ipſi .E. nihil valet, quia ſi inferius eſſet,
idem contingeret, ſed hoc euenit eo quod .E. altius eſt ipſo .b. Idem dico de .h.
vbi ſimiliter decipitur. Idem etiam in .7. cap. fallitur in ſecundo modo, quem oſten
dit pro ſecundo quadrato aliquo degradato à parallelogrammo degradato magis
longo quàm lato, cum ducat parallelam .l.m. ad .b.c. à puncto .l. interſection is ipſius .
o.c. id, quod non rectè efficitur quemadmodum ex rationibus à me allegatis circa
meas figuras .A.A. facilè innoteſcit.
tius quam .b. nempe eo quod .A. ſuperſtet ipſi .E. nihil valet, quia ſi inferius eſſet,
idem contingeret, ſed hoc euenit eo quod .E. altius eſt ipſo .b. Idem dico de .h.
vbi ſimiliter decipitur. Idem etiam in .7. cap. fallitur in ſecundo modo, quem oſten
dit pro ſecundo quadrato aliquo degradato à parallelogrammo degradato magis
longo quàm lato, cum ducat parallelam .l.m. ad .b.c. à puncto .l. interſection is ipſius .
o.c. id, quod non rectè efficitur quemadmodum ex rationibus à me allegatis circa
meas figuras .A.A. facilè innoteſcit.
Nono deinde cap. contrario planè ordine, quam oporteret proceſsit, quia cum
angulus .2. trianguli perfecti magis diſtet à plano ſuper quod degradari debet
triangulum, quàm latus .1. 3. oppoſitum dicto angulo .2. & per confequens longère
motior ſit ab oculo, ipſe in degradato, eum magis propinquum eſſe facit, è con-
tra eap .10. rectè fecit contra id, quod capite .9. tradiderat.
angulus .2. trianguli perfecti magis diſtet à plano ſuper quod degradari debet
triangulum, quàm latus .1. 3. oppoſitum dicto angulo .2. & per confequens longère
motior ſit ab oculo, ipſe in degradato, eum magis propinquum eſſe facit, è con-
tra eap .10. rectè fecit contra id, quod capite .9. tradiderat.
Quod autem deinceps in prima parte .11. & vltimi capitis aſſerit eſt, admittendum.
Quod verò in ſecunda parte ab eo traditur, ideſt alius quidam modus quem de tranſ
ferendis punctis à perfecto in degradato proponit, non eſt modus vniuerſalis; quia
ſi altitudo .T.Q. oculi à plano orizontali, non eſſet æqualis medietati lateris .B.D.
perfecti, interualla .a.b.c.d.e. lateris B.D. admittenda non eſſent.
Quod verò in ſecunda parte ab eo traditur, ideſt alius quidam modus quem de tranſ
ferendis punctis à perfecto in degradato proponit, non eſt modus vniuerſalis; quia
ſi altitudo .T.Q. oculi à plano orizontali, non eſſet æqualis medietati lateris .B.D.
perfecti, interualla .a.b.c.d.e. lateris B.D. admittenda non eſſent.
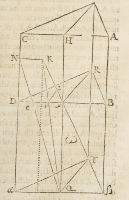
Pro cuius rei intelligentia ſit in ſubſcripta hic figura corporea .ω. parallelogram-
mum rectangulum A.B.C.D. in plano orizontali, & linea .Q.H. illud per medium
diuidat, quæ ſit parallela duobus lateribus .A.B. et .C.D. in cuius quolibet puncto .
Q. ſit infimus terminus altitudinis oculi, & in .
202[Figure 202]
T. ad perpendiculum ipſius .Q. ſit verus ſitus
eiuſdem, tantum eleuatus à .Q. quanta eſt
medietas ipſius .D.B. ſitq́ue figura corpo-
rea finita ſimilis meæ .A. vnde .Q.T. æqualis
erit ipſi .Q.æ. & planum perpendiculare orizon-
ti, ſuper quod punctum .k. perfecti duci debet
ſit .R.D.B. ſintq́ue ductæ per imaginationem
lineæ .T.K: Q.K. et ſit .K.N. perpendicularis la-
teri .C.D. à quo puncto .N. imaginatione ſit con
præhenſa linea .N.Q. at que hæ tres lineæ ſectæ
ſint à plano in punctis .c.i. et .2. quorum punctum.
2. erit quæſitum plani. Imaginemur nunc duos
triangulos .K.T.Q. et .N.Q.æ. qui ſecti erunt
à plano .R.B.D. quorum communes ſectiones
erunt .1. 2. et .D.c. & quia .N.K.D.i. et .æ.Q.
inuicem ſunt parallelæ, ſequitur eandem pro-
portionem futuram ipſius .Q.K. ad .K.i. quæ eſt
ipſius .æ.N. ad .N.D. imaginatione concipien
do a puncto .K. vſque ad .æ.Q. quandam paral-
lelam ipſi .N.æ. quemadmo dum ex te ipſo intel
ligere potes. Sed ratione ſimilitudinis trian-
gulorum ita ſe res habet de .æ.Q. ad .D.c. vt de .
æ.N. ad .N.D. vt quoque de .T.Q. ad .2. 1. quemadmodum ipſius .Q.K. ad .K.i. vn-
de ex .11. quinti, idem erit de .Q.T. ad .1. 2. quod de .Q.æ. ad .c.D. & ex .16. eiuſdem
de .Q.T. ad .Q.æ. quod de .1. 2. ad .c.D. & exiſtente .æ.Q. ex ſuppoſito æquali ipſi.
mum rectangulum A.B.C.D. in plano orizontali, & linea .Q.H. illud per medium
diuidat, quæ ſit parallela duobus lateribus .A.B. et .C.D. in cuius quolibet puncto .
Q. ſit infimus terminus altitudinis oculi, & in .
eiuſdem, tantum eleuatus à .Q. quanta eſt
medietas ipſius .D.B. ſitq́ue figura corpo-
rea finita ſimilis meæ .A. vnde .Q.T. æqualis
erit ipſi .Q.æ. & planum perpendiculare orizon-
ti, ſuper quod punctum .k. perfecti duci debet
ſit .R.D.B. ſintq́ue ductæ per imaginationem
lineæ .T.K: Q.K. et ſit .K.N. perpendicularis la-
teri .C.D. à quo puncto .N. imaginatione ſit con
præhenſa linea .N.Q. at que hæ tres lineæ ſectæ
ſint à plano in punctis .c.i. et .2. quorum punctum.
2. erit quæſitum plani. Imaginemur nunc duos
triangulos .K.T.Q. et .N.Q.æ. qui ſecti erunt
à plano .R.B.D. quorum communes ſectiones
erunt .1. 2. et .D.c. & quia .N.K.D.i. et .æ.Q.
inuicem ſunt parallelæ, ſequitur eandem pro-
portionem futuram ipſius .Q.K. ad .K.i. quæ eſt
ipſius .æ.N. ad .N.D. imaginatione concipien
do a puncto .K. vſque ad .æ.Q. quandam paral-
lelam ipſi .N.æ. quemadmo dum ex te ipſo intel
ligere potes. Sed ratione ſimilitudinis trian-
gulorum ita ſe res habet de .æ.Q. ad .D.c. vt de .
æ.N. ad .N.D. vt quoque de .T.Q. ad .2. 1. quemadmodum ipſius .Q.K. ad .K.i. vn-
de ex .11. quinti, idem erit de .Q.T. ad .1. 2. quod de .Q.æ. ad .c.D. & ex .16. eiuſdem
de .Q.T. ad .Q.æ. quod de .1. 2. ad .c.D. & exiſtente .æ.Q. ex ſuppoſito æquali ipſi.
zoom in
zoom out
zoom area
full page
page width
set mark
remove mark
get reference
digilib