15TABVLARVM SINVVM PER PET. APIANVM.
SEd ut nõnihil degenerali huius inſtrumẽti uſu dicamus, retulerit plurimũ, imò neceſ
ſariũ fuerit p̃mittere quædã, puta, ꝗd ſit Diameter, quid Chorda, quid etiã Sinus rect 9
11Diameter
quid.& quid ſituerſus. ? ?Diameter ſiue dimetiẽs circuli, eſt linea recta ꝑ eius umbilicum
trãſiens, illum´ in duo æqualia diuidens. ? ?Arcus eſt cuiuslibet circuli ſeu periferiæ
22Arcus. portio. ? ?Chorda eſt linea recta ſecãs circulũ in duas portiones inæquales. ? ?Sinus
33Chorda. eſt linea recta, diametro circuli lõgitudine uel potẽtia cõmenſurabilis. ? ?Sinus totus
44Sinus. ſiue ꝑfectus eſt circuli ſemidiameter in aliquas ꝑtes diuiſa. ? ?Sinus diuiditur in Sinum
55Sinus totus
ſiue perfe-
ctus quid. rectũ ac uerſum. ? ?Sinus rectus ſubdiuidit̃ in primũ & ſecũdũ. ? ?Sinus rectus pri-
mus eſt medietas chordæ arcus dupli ad arcũ, cuius eſt ſinus, ſiue dimidiũ chordæ reſpe-
ctu totius arcus. ? ?Sinus uerſus eſt portio diametri à ſinu recto ad periferiã cõprehen
66Sinus rect9
dupliater
diuiditur. ſi, utpote ſagitta arcus. ? ?Sinus rectus ſecũdus eſt reſiduũ cuiuslibet arc9 ſubtracti ex
90. ſiue arcus ꝗ reſtat uſ ad cõplementũ quartæ circuli, is ſemper eſt æqualis ꝑti dime
tientis, quæ à cẽtro circuli ad ſinũ rectũ primũ terminatur. ? ?Sector circuli eſt figura
77Sinus uerſ9
quid. q̃ continetur à duabus lineis recte à centro ad circumferentiã ductis, necnon ab arcu qui
88Sinus rect9
ſecundus. inter illos comprehẽditur. Verum hic quo teiſtud celare nolo, ꝙ inſtrumentũ hoc
oportet eſſe ſatis magnũ, omnino enim q̊ amplius fuerit, eò certius per illud operari pote
99Sector cir-
culi. ris. Quamuis ſi uoles, poteris q̊cũ alio numero ad hoc uti, alijs tamẽ cõmodiores ſunt
numeri, qui unitatẽ habent cũ aliquot nullis 000 & c. quales ſunt 10. 100. 1000. 10000.
100000 & c. ſiquidẽ per iſtos operatio nõ paulo redditur facilior in multiplicando pari
ter & diuidẽdo. Diuiſa igitur linea A B in hũc modũ, porrò circinũ altero pede repone
in A, alte℞ uero extẽde ad ſingula illa pũcta, extẽdens hoc pacto circinũ uſ ad ſemicir
culũ A F B, omnibus deinde illis in eũ circulũ ſinuũ redactis, numeros adſcribe incipien
do in B ꝑ F uſ ad A, ea´ dicentur puncta ſinus uerſi, quamobrẽ & ſemicirculus ille cir
culus appellabitur ſinus uerſi. Deinceps adductis iam punctis iſtis à linea A B uſ in cir
1010Vſus huius
ſemiarculi. culũ A F B, remoueri omnino aut deleri debet linea A B. uniuerſa aũt operatio illa ſatis
patebit ex ſubiecta figura. ? ?Seꝗtur ita uſus huius ſemicirculi in hunc modum: Si
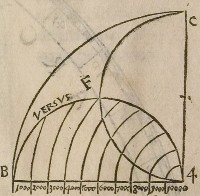 4[Figure 4]
quando ſinũ uerſum ſcire cupis cuiuslibet arcus, filũ in centro A adfixũ
4[Figure 4]
quando ſinũ uerſum ſcire cupis cuiuslibet arcus, filũ in centro A adfixũ
repone ſuper illũ gradum, & ſtatim ubicun filum iſtud ſemicirculum
AFB attingit, ibi uidebis numerũ unà cũ punctis ſinus illius uerſi. Vi
ciſsim cum antea habes puncta ſinus uerſi, & hinc deſideras arcum eius
cognoſcere, Age filum colloca ſuper illa puncta ſinus uerſi in ſemicir-
culo AFB, & eo quo filum tanget circulũ AC, ſcilicet limbum exteri
orem, ibi noris eſſe arcũ illorũ punctorũ ſinus uerſi propoſiti. Quod
ſi & alte℞ ſemicirculũ AFC cupis in pũcta ſinus recti diuidere, ſemper
tibi ꝓpone 10. aut 100 & c. ſecũdũ q̊d plura puncta habes in ſinu per-
fecto, hoc eſt in tota ſemidiametro AB. Vt ſi iã lineã AB in 100000.
partes habes diuiſam (nõ ꝙ totidẽ pũcta poſsis in ea conſignare, q̊rũ quodlibet ſignificet
unũ, ſed hoc ſatis eſt, ſi unũquod punctũ deſignet 100. aut 10. aut 5.) & porrò ſinũ re-
ctum 100000. punctorũ uis in circulũ AFC conſcribere, & cõprehendere in 100. pun-
ctis, ita, ꝙ unaquæ diuiſio cõprehendit 1000. tũc ſanè ſubtrahe 1000. à toto ſinu qui in
hoc exemplo eſſe debet 100000. & remanebũt 99000. qui ſinus erit uerſus, cuius ſi arcũ
ex ſupra dictis quæras, inuenies 88. gra. 26. mi. ea ſubtrahe à 90. & reſidui erũt o. gr. 34.
minut. Iam uero filũ repone ſuper o. gra. & 34. mi. numerãdo à Buerſus C, & in eũ locũ
quo tanget circulũ AFC, adponito punctũ 1000. puncta ſinus recti deſignans ex illis
100000. pũctis. Quod ſi aũt ſinus totus ſiue perfectus fuerit 10000. tũc punctũ illud ſi-
gnificat 100. rurſus ſi ſit ſinus perfectus 1000. punctũ hoc deſignabit 10. & ſi fuerit ſinus
perfectus 100. punctũ iſtud ſignabit unũ tantũ. At eo modo operaberis cum ſingulis
numeris prædictis, qñ locũ eius in ſemicirculo AFC quæris & ſcire deſideras. Mihi au
tem conſultiſsimũ eſſe uidetur, ſi ſemicirculũ illũ diuidas in 100. partes, ſicut hic ſeꝗtur.
Principio ſemidiametrũ AB diuide in 100. partes æquales, adſcribe etiã numeros ſingu
larũ partiũ occulte ꝑ quinarios uel denarios retrorſum à B in A at ea pũcta erunt ſinus
uerſi, q̃ deinde, modo quo ſupra diximus, transfer cũ circino in ſemicirculũ AFB, adſcri
bendo numeros q̊ pari modo ſicut in ſemidiametro AB feciſti. Mox pũcta ſimul &
ſariũ fuerit p̃mittere quædã, puta, ꝗd ſit Diameter, quid Chorda, quid etiã Sinus rect 9
11Diameter
quid.& quid ſituerſus. ? ?Diameter ſiue dimetiẽs circuli, eſt linea recta ꝑ eius umbilicum
trãſiens, illum´ in duo æqualia diuidens. ? ?Arcus eſt cuiuslibet circuli ſeu periferiæ
22Arcus. portio. ? ?Chorda eſt linea recta ſecãs circulũ in duas portiones inæquales. ? ?Sinus
33Chorda. eſt linea recta, diametro circuli lõgitudine uel potẽtia cõmenſurabilis. ? ?Sinus totus
44Sinus. ſiue ꝑfectus eſt circuli ſemidiameter in aliquas ꝑtes diuiſa. ? ?Sinus diuiditur in Sinum
55Sinus totus
ſiue perfe-
ctus quid. rectũ ac uerſum. ? ?Sinus rectus ſubdiuidit̃ in primũ & ſecũdũ. ? ?Sinus rectus pri-
mus eſt medietas chordæ arcus dupli ad arcũ, cuius eſt ſinus, ſiue dimidiũ chordæ reſpe-
ctu totius arcus. ? ?Sinus uerſus eſt portio diametri à ſinu recto ad periferiã cõprehen
66Sinus rect9
dupliater
diuiditur. ſi, utpote ſagitta arcus. ? ?Sinus rectus ſecũdus eſt reſiduũ cuiuslibet arc9 ſubtracti ex
90. ſiue arcus ꝗ reſtat uſ ad cõplementũ quartæ circuli, is ſemper eſt æqualis ꝑti dime
tientis, quæ à cẽtro circuli ad ſinũ rectũ primũ terminatur. ? ?Sector circuli eſt figura
77Sinus uerſ9
quid. q̃ continetur à duabus lineis recte à centro ad circumferentiã ductis, necnon ab arcu qui
88Sinus rect9
ſecundus. inter illos comprehẽditur. Verum hic quo teiſtud celare nolo, ꝙ inſtrumentũ hoc
oportet eſſe ſatis magnũ, omnino enim q̊ amplius fuerit, eò certius per illud operari pote
99Sector cir-
culi. ris. Quamuis ſi uoles, poteris q̊cũ alio numero ad hoc uti, alijs tamẽ cõmodiores ſunt
numeri, qui unitatẽ habent cũ aliquot nullis 000 & c. quales ſunt 10. 100. 1000. 10000.
100000 & c. ſiquidẽ per iſtos operatio nõ paulo redditur facilior in multiplicando pari
ter & diuidẽdo. Diuiſa igitur linea A B in hũc modũ, porrò circinũ altero pede repone
in A, alte℞ uero extẽde ad ſingula illa pũcta, extẽdens hoc pacto circinũ uſ ad ſemicir
culũ A F B, omnibus deinde illis in eũ circulũ ſinuũ redactis, numeros adſcribe incipien
do in B ꝑ F uſ ad A, ea´ dicentur puncta ſinus uerſi, quamobrẽ & ſemicirculus ille cir
culus appellabitur ſinus uerſi. Deinceps adductis iam punctis iſtis à linea A B uſ in cir
1010Vſus huius
ſemiarculi. culũ A F B, remoueri omnino aut deleri debet linea A B. uniuerſa aũt operatio illa ſatis
patebit ex ſubiecta figura. ? ?Seꝗtur ita uſus huius ſemicirculi in hunc modum: Si
repone ſuper illũ gradum, & ſtatim ubicun filum iſtud ſemicirculum
AFB attingit, ibi uidebis numerũ unà cũ punctis ſinus illius uerſi. Vi
ciſsim cum antea habes puncta ſinus uerſi, & hinc deſideras arcum eius
cognoſcere, Age filum colloca ſuper illa puncta ſinus uerſi in ſemicir-
culo AFB, & eo quo filum tanget circulũ AC, ſcilicet limbum exteri
orem, ibi noris eſſe arcũ illorũ punctorũ ſinus uerſi propoſiti. Quod
ſi & alte℞ ſemicirculũ AFC cupis in pũcta ſinus recti diuidere, ſemper
tibi ꝓpone 10. aut 100 & c. ſecũdũ q̊d plura puncta habes in ſinu per-
fecto, hoc eſt in tota ſemidiametro AB. Vt ſi iã lineã AB in 100000.
partes habes diuiſam (nõ ꝙ totidẽ pũcta poſsis in ea conſignare, q̊rũ quodlibet ſignificet
unũ, ſed hoc ſatis eſt, ſi unũquod punctũ deſignet 100. aut 10. aut 5.) & porrò ſinũ re-
ctum 100000. punctorũ uis in circulũ AFC conſcribere, & cõprehendere in 100. pun-
ctis, ita, ꝙ unaquæ diuiſio cõprehendit 1000. tũc ſanè ſubtrahe 1000. à toto ſinu qui in
hoc exemplo eſſe debet 100000. & remanebũt 99000. qui ſinus erit uerſus, cuius ſi arcũ
ex ſupra dictis quæras, inuenies 88. gra. 26. mi. ea ſubtrahe à 90. & reſidui erũt o. gr. 34.
minut. Iam uero filũ repone ſuper o. gra. & 34. mi. numerãdo à Buerſus C, & in eũ locũ
quo tanget circulũ AFC, adponito punctũ 1000. puncta ſinus recti deſignans ex illis
100000. pũctis. Quod ſi aũt ſinus totus ſiue perfectus fuerit 10000. tũc punctũ illud ſi-
gnificat 100. rurſus ſi ſit ſinus perfectus 1000. punctũ hoc deſignabit 10. & ſi fuerit ſinus
perfectus 100. punctũ iſtud ſignabit unũ tantũ. At eo modo operaberis cum ſingulis
numeris prædictis, qñ locũ eius in ſemicirculo AFC quæris & ſcire deſideras. Mihi au
tem conſultiſsimũ eſſe uidetur, ſi ſemicirculũ illũ diuidas in 100. partes, ſicut hic ſeꝗtur.
Principio ſemidiametrũ AB diuide in 100. partes æquales, adſcribe etiã numeros ſingu
larũ partiũ occulte ꝑ quinarios uel denarios retrorſum à B in A at ea pũcta erunt ſinus
uerſi, q̃ deinde, modo quo ſupra diximus, transfer cũ circino in ſemicirculũ AFB, adſcri
bendo numeros q̊ pari modo ſicut in ſemidiametro AB feciſti. Mox pũcta ſimul &
