152140IO. BAPT. BENED.
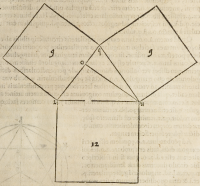
Ponamus nunc quadratum lateris .a.u. eſſe .12. clarum erit quodlibet quadratum
aliorum duorum laterum .a.q. et .u.q. futurum nouem, ex ijs quæ poſteriore loco dixi
mus, & quia quadratum ipſius .q.a. eſt tantò minus aliorum duorum quadratorum
ſumma, quantum eſt duplum producti ipſius .q.a. in .a.o. ex .13. ſecundi, ſed alia duo
quadrata ſimul collecta faciunt .21. à quo numero ſubtrahendo quadratum ipſius .a.
q. ideſt nouem, remanebit numerus .12. pro duplo producti ipſius .q.a. in .a.o. cuius
dupli me-
207[Figure 207]
dia pars, id-
eſt ſimplex
productum
ipſius .q.a.
in a.o. erit 6.
Sed quia qua
dratum ip-
ſius .q.a. eſt
nouem,
eius radix .
q.a. crit .3.
per quam di-
uidendo .6.
productum
ipſius .q.a.
in .a.o. pro
latere .a.o.
conſurgent
duo, cum er
go .a.o. ſint
duo tertia
ipſius .a.q.
certi erimus
a.o. eſſe latus dicti exagoni.
aliorum duorum laterum .a.q. et .u.q. futurum nouem, ex ijs quæ poſteriore loco dixi
mus, & quia quadratum ipſius .q.a. eſt tantò minus aliorum duorum quadratorum
ſumma, quantum eſt duplum producti ipſius .q.a. in .a.o. ex .13. ſecundi, ſed alia duo
quadrata ſimul collecta faciunt .21. à quo numero ſubtrahendo quadratum ipſius .a.
q. ideſt nouem, remanebit numerus .12. pro duplo producti ipſius .q.a. in .a.o. cuius
dupli me-
eſt ſimplex
productum
ipſius .q.a.
in a.o. erit 6.
Sed quia qua
dratum ip-
ſius .q.a. eſt
nouem,
eius radix .
q.a. crit .3.
per quam di-
uidendo .6.
productum
ipſius .q.a.
in .a.o. pro
latere .a.o.
conſurgent
duo, cum er
go .a.o. ſint
duo tertia
ipſius .a.q.
certi erimus
a.o. eſſe latus dicti exagoni.
CAP. XV.
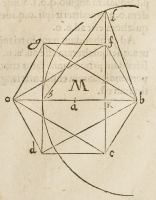
DEſiderantes ſcire deinde .l.k. in figura .M. quar
208[Figure 208]
ti cap. tertiæ partis perſpectiuę Danielis
Barbari, ſeu Zamberti, eſſe veram altitudinem cor-
poris octoaedri, primum ſcire debemus quod exiſtente .b.
h. vt etiam .b.l. tripla ad .b.k. vt ex ijs, quę ſuperius iam
diximus, facile percipi poteſt; ex penultima primi .
b.l. in potentia, ſeſquioctaua erit ad .k.l. ipſa et .k.
l. dupla inpotentia ad .h.k. & ob id ducta cum eſſet .h.
l. exiſteret in potentia tripla ad .h.k. & ſeſquialtera
ad .l.k. & ſeſquitertia ad .l.b. & ſic ad .h.b. vnde .l.h.
æqualis eſſet vni ex lateribus trianguli ęquilateri di-
cti corporis. Ex rationibus igitur ſuperius hîc poſi-
tis .l.k. erit altitudo dicta, id eſt diſtantia inter duas
facies inuicem oppoſitas, octoaedri.
Barbari, ſeu Zamberti, eſſe veram altitudinem cor-
poris octoaedri, primum ſcire debemus quod exiſtente .b.
h. vt etiam .b.l. tripla ad .b.k. vt ex ijs, quę ſuperius iam
diximus, facile percipi poteſt; ex penultima primi .
b.l. in potentia, ſeſquioctaua erit ad .k.l. ipſa et .k.
l. dupla inpotentia ad .h.k. & ob id ducta cum eſſet .h.
l. exiſteret in potentia tripla ad .h.k. & ſeſquialtera
ad .l.k. & ſeſquitertia ad .l.b. & ſic ad .h.b. vnde .l.h.
æqualis eſſet vni ex lateribus trianguli ęquilateri di-
cti corporis. Ex rationibus igitur ſuperius hîc poſi-
tis .l.k. erit altitudo dicta, id eſt diſtantia inter duas
facies inuicem oppoſitas, octoaedri.