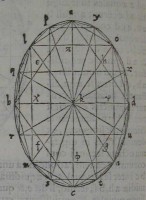
1triangulum mkφ triangulo nkφ. ergo anguli lzk, ozk,
m φ k, nφk æquales ſunt, ac recti. quòd cum etiam recti
ſint, qui ad k; æquidiſtabunt lineæ lo, mn axi bd. & ita
demonſtrabuntur lm, on ipſi ac æquidiſtare. Rurſus ſi
iungantur al, lb, bm, mc, cn, nd, do, oa: & bifariam di
uidantur: à centro autem k ad diuiſiones ductæ lineæ pro
trahantur uſque ad ſectionem in puncta pqrstuxy: & po
ſtremo py, qx, ru, st, qr, ps, yt, xu coniungantur. Simili
 8[Figure 8]
8[Figure 8]
ter oſtendemus lineas
py, qx, ru, st axi bd æ
quidiſtantes eſſe: & qr,
ps, yt, xu æquidiſtan
tes ipſi ac. Itaque dico
harum figurarum in el
lipſi deſcriptarum cen
trum grauitatis eſſe pun
ctum k, idem quod & el
lipſis centrum. quadri
lateri enim abcd cen
trum eſt k, ex decima e
iuſdem libri Archime
dis, quippe cum in eo om
nes diametri conueniant.
Sed in figura albmcn
do, quoniam trianguli
alb centrum grauitatis
eſt in linea le: trapezijque; abmo centrum in linea ek: trape
zij omcd in kg: & trianguli cnd in ipſa gn: erit magnitu
dinis ex his omnibus conſtantis, uidelicet totius figuræ cen
trum grauitatis in linea ln: & ob eandem cauſſam in linea
om. eſt enim trianguli aod centrum in linea oh: trapezij
alnd in hk: trapezij lbcn in kf: & trianguli bmc in fm.
cum ergo figuræ albmcndo centrum grauitatis ſit in li
nea ln, & in linea om; erit centrum ipſius punctum k, in
m φ k, nφk æquales ſunt, ac recti. quòd cum etiam recti
ſint, qui ad k; æquidiſtabunt lineæ lo, mn axi bd. & ita
demonſtrabuntur lm, on ipſi ac æquidiſtare. Rurſus ſi
iungantur al, lb, bm, mc, cn, nd, do, oa: & bifariam di
uidantur: à centro autem k ad diuiſiones ductæ lineæ pro
trahantur uſque ad ſectionem in puncta pqrstuxy: & po
ſtremo py, qx, ru, st, qr, ps, yt, xu coniungantur. Simili
 8[Figure 8]
8[Figure 8]ter oſtendemus lineas
py, qx, ru, st axi bd æ
quidiſtantes eſſe: & qr,
ps, yt, xu æquidiſtan
tes ipſi ac. Itaque dico
harum figurarum in el
lipſi deſcriptarum cen
trum grauitatis eſſe pun
ctum k, idem quod & el
lipſis centrum. quadri
lateri enim abcd cen
trum eſt k, ex decima e
iuſdem libri Archime
dis, quippe cum in eo om
nes diametri conueniant.
Sed in figura albmcn
do, quoniam trianguli
alb centrum grauitatis
eſt in linea le: trapezijque; abmo centrum in linea ek: trape
zij omcd in kg: & trianguli cnd in ipſa gn: erit magnitu
dinis ex his omnibus conſtantis, uidelicet totius figuræ cen
trum grauitatis in linea ln: & ob eandem cauſſam in linea
om. eſt enim trianguli aod centrum in linea oh: trapezij
alnd in hk: trapezij lbcn in kf: & trianguli bmc in fm.
cum ergo figuræ albmcndo centrum grauitatis ſit in li
nea ln, & in linea om; erit centrum ipſius punctum k, in
