Benedetti, Giovanni Battista de, Io. Baptistae Benedicti ... Diversarvm specvlationvm mathematicarum, et physicarum liber : quarum seriem sequens pagina indicabit ; [annotated and critiqued by Guidobaldo Del Monte]

Table of contents

< >
[3.3.] Quòd quantit as cuiuſlibet ponderis, aut uirtus mouens re-ſpectu alterius quantitatis cognoſcatur beneficio perpendicularium ductarum à centro libr & ad line am inclinationis. CAP. III.
Page: 155 (143)
[3.4.] Quemadmodum exſupradictis cauſis omnes staterarum & uectium cauſæ dependeant. CAP. IIII.
Page: 156 (144)
[3.5.] De quibuſdam rebus animaduerſione dignis. CAP.V.
Page: 157 (145)
[3.6.] De ratione cuiuſdam uis adauctæ. CAP. VI.
Page: 158 (146)
[3.7.] De quibuſdam erroribus Nicolai Tartaleæ circa pondera corporum & eorum motus, quorum aliqui deſumpti fuerunt à fordano ſcriptore quodam antiquo. CAP. VII.
Page: 160 (148)
[3.8.] CAP. VIII.
Page: 161 (149)
[3.9.] Quòdſummaratione ſtateræper æqualia interualla ſint diuiſæ. CAP. IX.
Page: 163 (151)
[3.10.] Quòd line a circularis non habe at concauum cum con-uexo coniunctum, & quod Aristo. cir caproportio nes motuum aberrauerit. CAP.X.
Page: 164 (152)
[3.11.] Quod Aristo. in prima mechanicarum quæstionum eius quod inquir it, uer am cauſam non attulerit. CAP. XI.
Page: 165 (153)
[3.12.] De uer a cauſa ſecundæ, & tertiæ quæstionis mechanicæ ab Ariſtotele nonperſpecta. CAP. XII.
Page: 166 (154)
[3.13.] Quòd Ariſtotelisratio in 6. quæſtione poſit a non ſit admittenda. CAP. XIII.
Page: 167 (155)
[3.14.] Quòdrationes ab Ariſtotele de octaua quæstione confictæ ſufficient es non ſint. CAP. XIIII.
Page: 167 (155)
[3.15.] Quod Aristotelis ratio none queſtionis admittendanon ſit. CAP. XV.
Page: 171 (159)
[3.16.] Quod Aristotelis rationes de decima queſtione ſint reijciende. CAP. XVI.
Page: 171 (159)
[3.17.] De uer a cauſa .12. questionis mechanice. CAP. XVII.
Page: 172 (160)
[3.18.] De decimatertia questione. CAP. XVIII.
Page: 173 (161)
[3.19.] De decimaquart a queſtione. CAP. XIX.
Page: 173 (161)
[3.20.] De uer a r atione .17. queſtionis. CAP. XX.
Page: 174 (162)
[3.21.] De uera & intrinſeca cauſa trocble arum. CAP. XXI.
Page: 175 (163)
[3.22.] Depropria cauſa .24. quæſtionis. CAP. XXII.
Page: 177 (165)
[3.23.] De uer a cauſa .30. quæstionis. CAP. XXIIII.
Page: 179 (167)
[3.24.] Deratione .35. & ultimæ quæstionis. CAP. XXV.
Page: 179 (167)
[4.] DISPVTATIONES DE QVIBVSDAM PLACITIS ARISTOTELIS.
Page: 180 (168)
[4.1.] Qualiter & ubi Ariſtoteles de uelocitate motuum natura-lium localium aliter tractauerit quam nos ſentiamus. CAP.I.
Page: 180 (168)
[4.2.] Quædam ſupponenda ut conſtet cur circa uelocit atem motuum natur alium localium ab Ariſtotelis placitis recedamus. CAP. II.
Page: 181 (169)
[4.3.] Poſſe uelocitatem alicuius corporis proportionem contrariam in diuerſis medijs habere cum denſitate eorum. CAP. III.
Page: 182 (170)
[4.4.] Oſcitanter ab Ariſtotele nonnibil prolatum cap 8. lib. 4 Phyſicorum. CAP. IIII.
Page: 182 (170)
[4.5.] Exempla dictorum. CAP.V.
Page: 183 (171)
[4.6.] Quod proportiones ponderum eiuſdem corporis in diuerſis medijs pro portiones eorum mediorum denſit atum non ſeruant. Unde ne-ceßariò inæquales proportiones uelocitatum producuntur. CAP. VI.
Page: 184 (172)
[4.7.] Corpora grauia aut leuia eiuſdem figur æ et materiæ ſed inæqualis magnitudinis, in ſuis motibus natur alibus uelocit atis, in eo dem medio, proportionem longè diuerſam ſeruatura eße quam Aristoteliuiſum fuerit. CAP. VII.
Page: 184 (172)
< >
page |< < (152) of 445 > >|
164152IO. BAPT. BENED.
CAP.X.
ARiſtoteles in principio quæſtionum Mechanicarum ait lineam, quæ terminat
1111[Handwritten note 11] circulum videtur conuexum habere coniunctum cum concauo, quod falſum
eſt: quia huiuſmodi linea partes nullas ſecundum latitudinem habet, (vt ipſe etiam
confirmat) ſed eſt idem conuexum circuli: linea verò quæ terminus eſt ſuperficiei
ambientis, & amplectentis circulum eſt eadem concauitas dictæ ſuperficiei eun-
dem circulum ambientis, quæ nullam conuexitatem habet. & hæ duæ ſunt lineæ,
quarum vna diuerſa eſt ab alia, neque altera alterius, quod ad conuexum, & ad con-
cauum attinet.
Sed illud, quod Ariſtoteles ſcribit de duplici reſpectu motus vnius puncti ſecun
dum vnam datam pro portionem, non ſufficit, ille enim ſic ait.
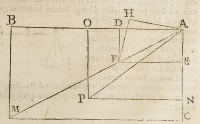
Sit proportio ſecundum quam latum fertur, quam habet .A.B. ad .A.C. et .A. qui
dem feratur verſus .B: A.B. verò ſubterferatur verſus .M.C. latum autem ſit .A. quidem
ad .D. vbi autem eſt .A.B. verſus .E. Quoniam igitur lationis erat proportio, quam .
A.B. habet ad .A.C. neceſſe eſt & .A.D. ad .A.E. hanc habere rationem. Simile igi
1212[Handwritten note 12] tur eſt pro portione paruum quadr ilaterum maiori. Quamobrem etc.
Cui reſpondeo, punctum .A. quod mouetur in linea .A.M. ab .A. verſus .M. vſque
ad .F. non moueriab aliqua proportione determinata magis quàm ab alia: vnde non
ſolum poſſumus imaginari dictum punctum .A. moueri ab .A. vſque ad .F. eiuſdem
velocitatis ſub alia quadam proportione, ſed etiam ſub alia, quæ iam datæ contraria
ſit, vt eſt proportio ipſius .A.C. ad .A.B. imaginantes moueri .A. verſus .C. et .A.C. ver
ſus .B.M. delatam. Dico etiam idem .A. moueri vſque ad .F. ſecundum proportio-
nem ipſius .A.O. ad .A.N. Quamobrem imaginemur à puncto .F. lineam .F.H. cum
linea .F.A. efficere angu-
lum æqualem angulo .O.
P.A. & à puncto .A. lineam
222[Figure 222] A.H. cum linea .A.F. face-
re angulum æqualem angulo
O.A.P. unde angulus .H.
æqualis erit angulo .O.
ex .32. libr. primi Eucl.
& triangulum .A.H.F. ęqui
angulum erit triangulo .
A.O.P. Quam ob causam
eadem proportio erit ipſius
A.H. ad .F.H. quę enipſius
A.O. ad .O.P. punctum
igitur .A. vſque ad .F. mouetur ſecundum proportionem etiam ipſius .A.O. ad .O.P.
Huiuſmodi igitur conſideratio, ab Ariſtotele facta, nullius eſt momenti.

Text layer

  • Dictionary

Text normalization

  • Original
  • Regularized
  • Normalized

Search


  • Exact
  • All forms
  • Fulltext index
  • Morphological index
Impressum