1oſcillationis unius, ut arcus HI(tempus quo corpus Hperveniet
ad L) ad ſemiperipheriam HKM(tempus quo corpus Hper
veniet ad M.) Et velocitas corporis penduli in loco Teſt ad ve
locitatem ipſius in loco infimo R,(hoc eſt, velocitas corporis Hin
loco Lad velocitatem ejus in loco G,ſeu incrementum momenta
neum lineæ HLad incrementum momentaneum lineæ HG,arcu
bus HI, HKæquabili fluxu creſcentibus) ut ordinatim applicata
LIad radium GK,ſive ut √SRq.-TRquead SR.Unde cum,
in oſcillationibus inæqualibus, deſcribantur æqualibus temporibus
arcus totis oſcillationum arcubus proportionales; habentur, ex da
tis temporibus, & velocitates & arcus deſcripti in oſcillationibus
univerſis. Quæ erant primo invenienda.
ad L) ad ſemiperipheriam HKM(tempus quo corpus Hper
veniet ad M.) Et velocitas corporis penduli in loco Teſt ad ve
locitatem ipſius in loco infimo R,(hoc eſt, velocitas corporis Hin
loco Lad velocitatem ejus in loco G,ſeu incrementum momenta
neum lineæ HLad incrementum momentaneum lineæ HG,arcu
bus HI, HKæquabili fluxu creſcentibus) ut ordinatim applicata
LIad radium GK,ſive ut √SRq.-TRquead SR.Unde cum,
in oſcillationibus inæqualibus, deſcribantur æqualibus temporibus
arcus totis oſcillationum arcubus proportionales; habentur, ex da
tis temporibus, & velocitates & arcus deſcripti in oſcillationibus
univerſis. Quæ erant primo invenienda.
LIBER
PRIMUS.
PRIMUS.
Oſcillentur jam Funipendula
 100[Figure 100]
100[Figure 100]
corpora in Cycloidibus diverſis
intra Globos diverſos, quorum
diverſæ ſunt etiam Vires abſolu
tæ, deſcriptis: &, ſi Vis abſolu
ta Globi cujuſvis QOSdicatur V,
Vis acceleratrix qua Pendulum urge
tur in circumferentia hujus Globi,
ubi incipit directe verſus centrum
ejus moveri, erit ut diſtantia Cor
poris penduli a centro illo & Vis abſoluta Globi conjunctim, hoc
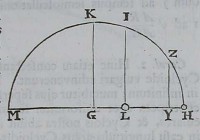
eſt, ut COXV. Itaque lineola HY,quæ ſit ut hæc Vis accelera
trix COXV, deſcribetur dato tempore; &, ſi erigatur normalis YZ
circumferentiæ occurrens in Z,arcus naſcens HZdenotabit datum
illud tempus. Eſt autem arcus hic naſcens HZin ſubduplicata ra
tione rectanguli GHY,adeoque ut √GHXCOXV. Unde Tem
pus oſcillationis integræ in Cycloide QRS(cum ſit ut ſemiperi
pheria HKM,quæ oſcillationem illam integram denotat, directe,
utque arcus HZ,qui datum tempus ſimiliter denotat, inverſe) fiet
ut GHdirecte & √GHXCOXV inverſe, hoc eſt, ob æquales GH
& SR,ut √(SR/COXV), ſive (per Corol. Prop. L) ut √(AR/ACXV).
Itaque Oſcillationes in Globis & Cycloidibus omnibus, quibuſ
cunque cum Viribus abſolutis factæ, ſunt in ratione quæ compo
nitur ex ſubduplicata ratione longitudinis Fili directe, & ſubdu
plicata ratione diſtantiæ inter punctum ſuſpenſionis & centrum
 100[Figure 100]
100[Figure 100]corpora in Cycloidibus diverſis
intra Globos diverſos, quorum
diverſæ ſunt etiam Vires abſolu
tæ, deſcriptis: &, ſi Vis abſolu
ta Globi cujuſvis QOSdicatur V,
Vis acceleratrix qua Pendulum urge
tur in circumferentia hujus Globi,
ubi incipit directe verſus centrum
ejus moveri, erit ut diſtantia Cor
poris penduli a centro illo & Vis abſoluta Globi conjunctim, hoc
eſt, ut COXV. Itaque lineola HY,quæ ſit ut hæc Vis accelera
trix COXV, deſcribetur dato tempore; &, ſi erigatur normalis YZ
circumferentiæ occurrens in Z,arcus naſcens HZdenotabit datum
illud tempus. Eſt autem arcus hic naſcens HZin ſubduplicata ra
tione rectanguli GHY,adeoque ut √GHXCOXV. Unde Tem
pus oſcillationis integræ in Cycloide QRS(cum ſit ut ſemiperi
pheria HKM,quæ oſcillationem illam integram denotat, directe,
utque arcus HZ,qui datum tempus ſimiliter denotat, inverſe) fiet
ut GHdirecte & √GHXCOXV inverſe, hoc eſt, ob æquales GH
& SR,ut √(SR/COXV), ſive (per Corol. Prop. L) ut √(AR/ACXV).
Itaque Oſcillationes in Globis & Cycloidibus omnibus, quibuſ
cunque cum Viribus abſolutis factæ, ſunt in ratione quæ compo
nitur ex ſubduplicata ratione longitudinis Fili directe, & ſubdu
plicata ratione diſtantiæ inter punctum ſuſpenſionis & centrum
