Commandino, Federico - Liber de centro gravitatis solidorum

Commandino, Federico, Liber de centro gravitatis solidorum, 1565

Table of figures

[Figure 11]

[Figure 12]

[Figure 13]

[Figure 14]

[Figure 15]

[Figure 16]

[Figure 17]

[Figure 18]

[Figure 19]

[Figure 20]

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

1teſt in portione, quæ recta linea & obtuſianguli coni ſe
ctione, ſeu hyperbola continetur.

THEOREMA IIII. PROPOSITIO IIII.

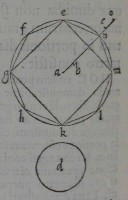
IN circulo & ellipſi idem eſt figuræ & graui
tatis centrum.

SIT circulus, uel ellipſis, cuius centrum a. Dico a gra
uitatis quoque centrum eſſe. Si enim fieri poteſt, ſit b cen
trum grauitatis: & iuncta ab extra figuram in c produca
tur: quam uero proportionem habet linea ca ad ab, ha
beat circulus a ad alium circulum, in quo d; uel ellipſis ad
aliam ellipſim: & in circulo, uel ellipſi figura rectilinea pla
ne deſcribatur adco, ut tandem relinquantur portiones
quædam minores circulo, uel ellipſi d; quæ figura ſit abcefg
hklmn. Illud uero in circulo fieri poſſe ex duodecimo
elementorum libro, propoſitione ſecunda manifeſte con

10[Figure 10]
ſtat; at in ellipſi nos demonſtra
uimus in commentariis in quin
tam propoſitionem Archimedis
de conoidibus, & ſphæroidibus.
erit igitur a centrum grauitatis
ipſius figuræ, quod proxime oſten
dimus. Itaque quoniam circulus
a ad circulum d, uel ellipſis a ad
ellipſim d eandem proportionem
habet, quam linea ca ad ab:
portiones uero ſunt minores cir

culo uel ellipſi d: habebit circu
lus, uel ellipſis ad portiones ma
iorem proportionem, quàm ca

ad ab: & diuidendo figura recti
linea abcefghklmn ad portiones

Text layer

Text normalization

Search