Commandino, Federico - Liber de centro gravitatis solidorum

Commandino, Federico, Liber de centro gravitatis solidorum, 1565

Table of figures

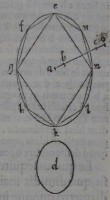[Figure 11]

[Figure 12]

[Figure 13]

[Figure 14]

[Figure 15]

[Figure 16]

[Figure 17]

[Figure 18]

[Figure 19]

[Figure 20]

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

1

11[Figure 11]
habebit maiorem proportionem,
quam cb ad ba. fiat ob ad ba,
ut figura rectilinea ad portio
nes. cum igitur à circulo, uel el
lipſi, cuius grauitatis centrum
eſt b, auferatur figura rectilinea
efghklmn, cuius centrum a;
reliquæ magnitudinis ex portio

nibus compoſitæ centrum graui
tatis erit in linea ab producta,
& in puncto o, extra figuram po
ſito. quod quidem fieri nullo mo
do poſſe perſpicuum eſt. ſequi
tur ergo, ut circuli & ellipſis cen
trum grauitatis ſit punctum a,
idem quod figuræ centrum.

8. quinti

19. quinti
apud Cam
panum .

8. Archi
medis.

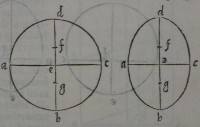
Sit circulus, uel ellipſis abcd,
cuius diameter db, & centrum e: ducaturque per e recta li
nea ac, ſecans ipſam db ad rectos angulos. erunt adc,
abc circuli, uel ellipſis dimidiæ portiones. Itaque quo

12[Figure 12]
niam por
tionis adc
centrum gra
uitatis eſt
in diame
tro de: &
portionis
abc cen
trum eſt im
ipſa eb: to
tius circu
li, uel ellipſis grauitatis centrum erit in diametro db.
Sit autem portionis adc centrum grauitatis f: & ſumatur

Text layer

Text normalization

Search