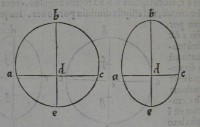
1in linea eb punctum g, ita ut fit ge æqualis ef.
erit g por
tionis abc centrum. nam ſi hæ portiones, quæ æquales
& ſimiles ſunt, inter ſe ſe aptentur, ita ut be cadat in de,
& punctum b in d cadet, & g in f: figuris autem æquali
bus, & ſimilibus inter ſe aptatis, centra quoque grauitatis
ipſarum inter ſe aptata erunt, ex quinta petitione Archi
medis in libro de centro grauitatis planorum. Quare cum
portionis adc centrum grauitatis ſit f: & portionis
abc centrum g: magnitudinis; quæ ex utriſque efficitur:
hoc eſt circuli uel ellipſis grauitatis centrum in medio li
neæ fg, quod eſt e, conſiſtet, ex quarta propoſitione eiuſ
dem libri Archimedis. ergo circuli, uel ellipſis centrum
grauitatis eſt idem, quod figuræ centrum. atque illud eſt,
quod demonſtrare oportebat.
tionis abc centrum. nam ſi hæ portiones, quæ æquales
& ſimiles ſunt, inter ſe ſe aptentur, ita ut be cadat in de,
& punctum b in d cadet, & g in f: figuris autem æquali
bus, & ſimilibus inter ſe aptatis, centra quoque grauitatis
ipſarum inter ſe aptata erunt, ex quinta petitione Archi
medis in libro de centro grauitatis planorum. Quare cum
portionis adc centrum grauitatis ſit f: & portionis
abc centrum g: magnitudinis; quæ ex utriſque efficitur:
hoc eſt circuli uel ellipſis grauitatis centrum in medio li
neæ fg, quod eſt e, conſiſtet, ex quarta propoſitione eiuſ
dem libri Archimedis. ergo circuli, uel ellipſis centrum
grauitatis eſt idem, quod figuræ centrum. atque illud eſt,
quod demonſtrare oportebat.
Ex quibus ſequitur portionis circuli, uel ellip
ſis, quæ dimidia maior ſit, centrum grauitatis in
diametro quoque ipſius conſiſtere.
ſis, quæ dimidia maior ſit, centrum grauitatis in
diametro quoque ipſius conſiſtere.
 13[Figure 13]
13[Figure 13]
