1
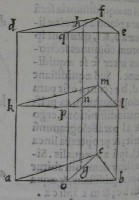
Itaque quoniam duæ lineæ Kl, lm ſe ſe tangentes, duabus
lineis ſe ſe tangentibus ab, bc æquidiſtant; nec ſunt in e o
dem plano: angulus klm æqualis eſt angulo abc: & ita an
gulus lmk, angulo bca, & mkl ipſi cab æqualis probabi
tur. triangulum ergo klm eſt æquale, & ſimile triangulo
abc. quare & triangulo def. Ducatur linea cgo, & per ip
ſam, & per cf ducatur planum ſecans priſma; cuius & paral
lelogrammi ae communis ſectio ſit opq. tranſibit linea
fq per h, & mp per n. nam cum plana æquidiſtantia ſecen
tur à plano cq, communes eorum ſectiones cgo, mp, fq
ſibi ipſis æquidiſtabunt. Sed & æquidiſtant ab, kl, de. an
guli ergo aoc, kpm, dqf inter ſe æquales ſunt: & ſunt
æquales qui ad puncta akd conſtituuntur. quare & reliqui
reliquis æquales; & triangula aco, Kmp, dfq inter ſe ſimi
lia erunt. Vt igitur ca ad ao, ita fd ad dq: & permutando
ut ca ad fd, ita ao ad dq. eſt autem ca æqualis fd. ergo &
ao ipſi dq. eadem quoque ratione & ao ipſi Kp æqualis
demonſtrabitur. Itaque ſi triangula, abc, def æqualia &
 15[Figure 15]
15[Figure 15]
ſimilia inter ſe aptentur,
cadet linea fq in lineam
cgo. Sed & centrum gra
uitatis h in g centrum ca
det. tranſibit igitur linea
fq per h: & planum per
co & cf ductum per axem
gh ducetur: idcircoque li
neam mp etiam per n tran
ſire neceſſe erit. Quo
niam ergo fh, cg æqua
les ſunt, & æquidiſtantes:
itemque hq, go; rectæ li
neæ, quæ ipſas connectunt
cmf, gnh, opq æqua
les æquidiſtantes erunt.
lineis ſe ſe tangentibus ab, bc æquidiſtant; nec ſunt in e o
dem plano: angulus klm æqualis eſt angulo abc: & ita an
gulus lmk, angulo bca, & mkl ipſi cab æqualis probabi
tur. triangulum ergo klm eſt æquale, & ſimile triangulo
abc. quare & triangulo def. Ducatur linea cgo, & per ip
ſam, & per cf ducatur planum ſecans priſma; cuius & paral
lelogrammi ae communis ſectio ſit opq. tranſibit linea
fq per h, & mp per n. nam cum plana æquidiſtantia ſecen
tur à plano cq, communes eorum ſectiones cgo, mp, fq
ſibi ipſis æquidiſtabunt. Sed & æquidiſtant ab, kl, de. an
guli ergo aoc, kpm, dqf inter ſe æquales ſunt: & ſunt
æquales qui ad puncta akd conſtituuntur. quare & reliqui
reliquis æquales; & triangula aco, Kmp, dfq inter ſe ſimi
lia erunt. Vt igitur ca ad ao, ita fd ad dq: & permutando
ut ca ad fd, ita ao ad dq. eſt autem ca æqualis fd. ergo &
ao ipſi dq. eadem quoque ratione & ao ipſi Kp æqualis
demonſtrabitur. Itaque ſi triangula, abc, def æqualia &
 15[Figure 15]
15[Figure 15]ſimilia inter ſe aptentur,
cadet linea fq in lineam
cgo. Sed & centrum gra
uitatis h in g centrum ca
det. tranſibit igitur linea
fq per h: & planum per
co & cf ductum per axem
gh ducetur: idcircoque li
neam mp etiam per n tran
ſire neceſſe erit. Quo
niam ergo fh, cg æqua
les ſunt, & æquidiſtantes:
itemque hq, go; rectæ li
neæ, quæ ipſas connectunt
cmf, gnh, opq æqua
les æquidiſtantes erunt.
