Commandino, Federico - Liber de centro gravitatis solidorum

Commandino, Federico, Liber de centro gravitatis solidorum, 1565

Table of figures

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

[Figure 41]

[Figure 42]

[Figure 43]

[Figure 44]

[Figure 45]

[Figure 46]

[Figure 47]

[Figure 48]

[Figure 49]

[Figure 50]

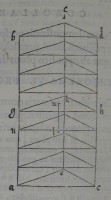
1 ergo linea ag continenter in duas partes æquales diui
ſa, relinquetur tandem pars aliqua ng, quæ minor erit lm.
Vtraque uero linearum ag, gb diuidatur in partes æqua
les ipſi ng: & per puncta diuiſionum plana oppoſitis pla

nis æquidiſtantia ducantur. erunt ſectiones figuræ æqua
les, ac ſimiles ipſis ace, bdf: & totum priſma diuiſum erit
in priſmata æqualia, & ſimilia: quæ cum inter ſe congruant;
& grauitatis centra ſibi ipſis congruentia, reſpondentiaque

16[Figure 16]
habebunt. Itaque
ſunt magnitudi
nes quædam æqua
les ipſi nh, & nu
mero pares, qua
rum centra gra
uitatis in eadem re
cta linea conſti
tuuntur: duæ ue
ro mediæ æqua
les ſunt: & quæ ex
utraque parte i
pſarum ſimili
ter æquales: & æ
quales rectæ li
neæ, quæ inter
grauitatis centra
interiiciuntur.
quare ex corolla
rio quintæ pro
poſitionis primi
libri Archimedis
de centro graui
tatis planorum; magnitudinis ex his omnibus compoſitæ
centrum grauitatis eſt in medio lineæ, quæ magnitudi
num mediarum centra coniungit. at qui non ita res

Text layer

Text normalization

Search