Benedetti, Giovanni Battista de - Io. Baptistae Benedicti ... Diversarvm specvlationvm mathematicarum, et physicarum liber : quarum seriem sequens pagina indicabit ; [annotated and critiqued by Guidobaldo Del Monte]

Scan	Original
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108
121	109
122	110
123	111
124	112
125	113
126	114
127	115
128	116
129	117
130	118

258246IO. BAPT. BENED. præciſe ideſt interuallum inter centrum mundi, & centrum epicycli Martis in huiuſ-
modi ſitu.

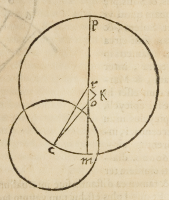
Fingemus igitur eccenticum Martis ſignificatum per .p.c.m. cuius centrum ſit .r.
& lineam augis .p.r.o.m. in qua centrum mundi ſit .o. centrum autem verum epicycli,
comprehendatur ab angulo .p.o.c. qui ſit graduum .151. min .30. ſecundum ſuppoſi-
tum. Quare in puncto .c. erit centrum epicycli. Imaginemur ergo .c.o. productam à
parte .o. quouſque ab .r. centro deferentis veniat linea .r.k. perpendiculariter, faciens
angulum rectum in puncto. k & quoniam angulus .r.o.c. datur nobis graduum .151.
min .30. ideo cognoſcemus angulum .r.o.k. tanquam reliquum ex duobus rectis, qui
erit gra .28. min .30. & ſimiliter angu-

293[Figure 293] lum .o.r.k. tanquam reſiduum vnius
recti, qui erit gra .61. min .30. cuius ſi-
nus ideſt .o.k. erit partium .8788 1. et .k.
r. vt ſinus anguli .r.o.k. partium .47715
talium qualium .o.r. eſſet 100000. ſed
vt .o.r. eſt .6. latus .o.k. erit .5. & min .16
et .r.k. partium .2. min .52. & quia .r.c.
cſt partium 60. eiuſmodi, ſi ab eius qua-
drato ſubtractum fuerit quadratum ip
ſius .r.k. reliquum erit nobis quadratum
ipſius .k.c. cuius radix, ideſt .k. erit par-
tium .59. min .56. à qua .c.k. ſubtrahen-
do poſtea .k.o. partium .5. minu .16. re-
manebit .o.c. partium .54. min .40. pro
diſtantia quæſita.

Fingamus poſtea epicyclum .f.n.g.
in quo argumentum verum graduum .
149. minu .39. ſit arcus .f.n. vbi Mars inueniatur in .n. per quem punctum tranſeat li-
nea .o.n. veri motus Martis. Deinde inueniamus angulum .c.o.n. æquationis argumem
ti, modo iam dicto, ideſt ducendo ſinum .n.h. arcus .n.g. qui arcus tanquam reliquus
argumenti veri, iam præſuppoſiti, ex dimidio circulo, erit graduum 30. minu .21. &
n.h. eius ſinus partium .50528. ſinus ſimiliter anguli .n.c.h. et .c.h. tanquam ſinus an-
guli .c.n.h. reſtantis ex uno recto grad .59. minu .39. erit partium .86295. talium qua-
lium .c.n. ſinus totus eſſet partium .100000. ſed vt partium .39. & min .30. ſinus .c.h.
erit partium .34. min .5. et .n.h. partium .19. mi .57. reliquum poſtea .h.o. ex .o.c. par-
tium .20. min .35. quia iam ſupra inuenimus .o.c. eſſe partium eiuſmodi .54. minu .40.
vnde .o.n. vt radix quadrata ſummæ duorum .n.h. et .h.o. erit partium .28. minu .41.
talium qualium .n.h. inuenta fuit partium .19. min .57. quæ .n.h. erit poſtea partium,
69552. talium qualium .n.o. partium .100000. & ſumpta dicta .n.h. vt ſinus dictarum
partium, dabit nobis angulum .n.o.h. quæſitum gra .44. min .4. qui per tabulas Alfon
ſi inuentus eſt gra .44. min .2. par huic, vt dici poteſt. Quiangulus gra .44. minu .4.
collectus cum angulo veri centri iam ſuppoſito graduum .151. minu .20. & cum an-
gulo augis eccentrici Martis, ſimiliter ſuppoſitæ grad .135. min .5. dabit nobis ſum-
mam veræ diſtantiæ Martis à principio Arietis grad .330. min .29. quod aliud non
ſignificat, niſi quod Mars inuenietur in minu .29. primi gradus Piſcium. Et Stofle-
rus in ſuis ephemeridibus ponit eum in .22. minuto dicti primi gradus, cuius diffe-

Page concordance

Text layer

Text normalization

Search

Scan	Original
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108
121	109
122	110
123	111
124	112
125	113
126	114
127	115
128	116
129	117
130	118

Scan	Original
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108
121	109
122	110
123	111
124	112
125	113
126	114
127	115
128	116
129	117
130	118

Scan	Original
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108
121	109
122	110
123	111
124	112
125	113
126	114
127	115
128	116
129	117
130	118