Commandino, Federico - Liber de centro gravitatis solidorum

Commandino, Federico, Liber de centro gravitatis solidorum, 1565

Table of figures

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

[Figure 41]

[Figure 42]

[Figure 43]

[Figure 44]

[Figure 45]

[Figure 46]

[Figure 47]

[Figure 48]

[Figure 49]

[Figure 50]

1

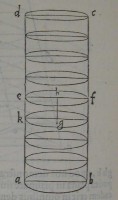
SIT cylindrus, uel cylindri portio ac: & plano per a
xem ducto ſecetur; cuius ſectio ſit parallelogrammum ab
cd: & bifariam diuiſis ad, bc parallelogrammi lateribus,
per diuiſionum puncta ef planum baſi æquidiſtans duca
tur; quod faciet ſectionem, in cylindro quidem circulum
æqualem iis, qui ſunt in baſibus, ut demonſtrauit Serenus
in libro cylindricorum, propoſitione quinta: in cylindri
uero portione ellipſim æqualem, & ſimilem eis, quæ ſunt

18[Figure 18]
in oppoſitis planis, quod nos
demonſtrauimus in commen
tariis in librum Archimedis
de conoidibus, & ſphæroidi
bus. Dico centrum grauita
tis cylindri, uel cylindri por
tionis eſſe in plano ef. Si enim
fieri poteſt, fit centrum g: &
ducatur gh ipſi ad æquidi
ſtans, uſque ad ef planum.
Itaque linea ae continenter
diuiſa bifariam, erit tandem
pars aliqua ipſius ke, minor
gh. Diuidantur ergo lineæ
ae, ed in partes æquales ipſi
ke: & per diuiſiones plana ba
ſibus æquidiſtantia ducantur.
erunt iam ſectiones, figuræ æ
quales, & ſimiles eis, quæ ſunt
in baſibus: atque erit cylindrus in cylindros diuiſus: & cy
lindri portio in portiones æquales, & ſimiles ipſi kf. reli
qua ſimiliter, ut ſuperius in priſmate concludentur.

Text layer

Text normalization

Search