277265EPISTOLAE.
De inuentione axis propoſite portionis datæ ſphæræ.
AD EVNDEM.
VTaxem propoſitæ alicuius datæ ſphæræ inuenire poſſis ita tibi operandum eſt
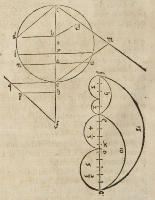
vt gratia exempli. Propoſita nobis eſt ſphæra .c.i.e.t. diametri cognitæ. pro
poſita etiam eſt nobis eius portio .n.e.u. axis .e.a. cognitæ minoris ſemidiametro, da-
ta etiam nobis eſt proportio alterius portionis minoris hemiſphærio .i.e.t. ad por-
tionem .n.e.u. quæritur nunc quantus ſit axis .e.x. ſecundæ portionis hoc eſt deſidera-
mus cognoſcere proportionem .e.x. ad .e.a. vel ad diametrum ipſius ſpheræ.
vt gratia exempli. Propoſita nobis eſt ſphæra .c.i.e.t. diametri cognitæ. pro
poſita etiam eſt nobis eius portio .n.e.u. axis .e.a. cognitæ minoris ſemidiametro, da-
ta etiam nobis eſt proportio alterius portionis minoris hemiſphærio .i.e.t. ad por-
tionem .n.e.u. quæritur nunc quantus ſit axis .e.x. ſecundæ portionis hoc eſt deſidera-
mus cognoſcere proportionem .e.x. ad .e.a. vel ad diametrum ipſius ſpheræ.
Cuius gratia reperiatur primò proportio circunferentiæ maioris circuli ipſius ſphae
ræ adeius diametrum, quæ ferè eſt vt .22. ad .7. ex Archimede.
ræ adeius diametrum, quæ ferè eſt vt .22. ad .7. ex Archimede.
Quo facto, inueniatur quantitas ſuperficialis huiuſmodi maioris circuli, quæ ſem-
per æqualis eſt producto quod fit ex ſemidiametro in dimidium circunferentiæ ip-
fius circuli, ex eodem Archimede. Et ſic cognoſcemus quartam partem ſuperficiei
ſphæricæ ſphærę propoſite ex .31. primi lib. de ſphæra, & cyllindro Archimedis.
per æqualis eſt producto quod fit ex ſemidiametro in dimidium circunferentiæ ip-
fius circuli, ex eodem Archimede. Et ſic cognoſcemus quartam partem ſuperficiei
ſphæricæ ſphærę propoſite ex .31. primi lib. de ſphæra, & cyllindro Archimedis.
Deinde ſumatur tertia pars producti, quod fit ex ſemidiametro in ſuperficiem
maioris circuli, & habebimus conum, cuius baſis erit circulus maior, altitudo verò
ſemidiameter propoſitæ ſphæræ ex .9. duodecimi Eucli.
maioris circuli, & habebimus conum, cuius baſis erit circulus maior, altitudo verò
ſemidiameter propoſitæ ſphæræ ex .9. duodecimi Eucli.
Quadruplum poſtea huiuſmodi coni, erit quantitas ſoliditatis, ſeu corporeitas to
tius ſphærę ex .32. dicti lib. Archimedis.
tius ſphærę ex .32. dicti lib. Archimedis.
Imaginemur poſtea in ſphærica portione .n.e.u. lineam .e.u. à summitate ad extremitatem
baſis, cuius .e.u. quantitatem cognoſcemus, hoc modo ſcilicet, fumendo radicem qua-
dratam producti .c.e. in .e.a. eo quod
quadratum .e.u. æquale eſt quadrato
 308[Figure 308]
a.u. & quadrato .a.e. ex penultima
308[Figure 308]
a.u. & quadrato .a.e. ex penultima
primi Eucli. hoc eſt producto quod
fit ex .c.a. in .a.e. ex .34. tertij eiuſdem,
& quadrato .a.e. hoc eſt producto,
quod fit ex .c.e. in .e.a. ex .3. ſecundi
eiuſdem.
baſis, cuius .e.u. quantitatem cognoſcemus, hoc modo ſcilicet, fumendo radicem qua-
dratam producti .c.e. in .e.a. eo quod
quadratum .e.u. æquale eſt quadrato
primi Eucli. hoc eſt producto quod
fit ex .c.a. in .a.e. ex .34. tertij eiuſdem,
& quadrato .a.e. hoc eſt producto,
quod fit ex .c.e. in .e.a. ex .3. ſecundi
eiuſdem.
Inuenta poſtea .e.u. ponamus eam
vnius circuli ſemidiametrum eſſe, cu
ius ſuperficialis quantitas etiam inue
niatur, vt ſupra dictum eſt, quæ qui
dem æqualis erit ſuperficiei portionis
n.e.u. ex .40. primi li. Archimedis de
ſphæra, & cyllindro.
vnius circuli ſemidiametrum eſſe, cu
ius ſuperficialis quantitas etiam inue
niatur, vt ſupra dictum eſt, quæ qui
dem æqualis erit ſuperficiei portionis
n.e.u. ex .40. primi li. Archimedis de
ſphæra, & cyllindro.
Hæc autem quantitas vltimo inuem
ta multiplicetur cum tertia parte ſe-
midiametri datæ ſphæræ, & habebi-
mus ſoliditatem vnius coni æqualis
aggregato ſoliditatis portionis .n.e.
u. ſimul ſumptę, cum ſoliditate vnius co
ni, cuius axis ſit .a.o. reſiduum ſemidia-
metri noſtræ ſphæræ dempta .a.e. ba
ta multiplicetur cum tertia parte ſe-
midiametri datæ ſphæræ, & habebi-
mus ſoliditatem vnius coni æqualis
aggregato ſoliditatis portionis .n.e.
u. ſimul ſumptę, cum ſoliditate vnius co
ni, cuius axis ſit .a.o. reſiduum ſemidia-
metri noſtræ ſphæræ dempta .a.e. ba
