314302IO. BABPT. BENED.
ELIPSIM PROPOSITAM QVALITER
quadrare valeamus.
Illuſtri Uiro Franciſco Mendo Zzæ
QVod antea tuo nomine fecerat Marcus Antonius amicus noſter ſufficie-
bat. Sed quia, quæ nunc à me petis, talia ſunt, vt ſine tripartita aequa-
liter aliqua data proportione non poſſit aliquis exactè intentum perfice-
re, nihilominus, ſuppoſita di
 335[Figure 335]
cta diuiſione, reliqua facilia erunt.
Primum
335[Figure 335]
cta diuiſione, reliqua facilia erunt.
Primum
enim eſt. Propoſitam Ellipſim qua-
drare.
bat. Sed quia, quæ nunc à me petis, talia ſunt, vt ſine tripartita aequa-
liter aliqua data proportione non poſſit aliquis exactè intentum perfice-
re, nihilominus, ſuppoſita di
enim eſt. Propoſitam Ellipſim qua-
drare.
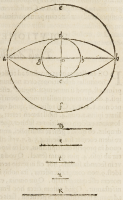
Sit igitur Ellipſis propoſita .a.b.d.c. cu-
ius axes ſint .a.b. et .d.c. dati, ſeu reperti ex
47. ſecundi Pergei, ſintque; duo circuli .a.e.
b.f. et .g.d.h.c. circa eaſdem diametros,
tunc proportio .a.b. ad .d.c. dimidium erit
proportionis circulorum ex .2. 12. Eu-
clid. ſed proportio .a.b. ad .d.c. æqualis
eſt proportioni maioris circuli ad Elli
pſim .ex .5. Archimedis in lib. de cono
idalibus, quapropter proportio Elli-
pſis ad minorem circulum altera me-
dietas erit totius proportionis circulo-
rum, hoc eſt maioris ad minorem, qua
re Ellipſis media proportionalis erit
inter eos circulos. Nunc verò cum
ex Archimede repertę fuerint duæ fi-
guræ rectilineæ æquales duobus circu
lis iam dictis, & inter has, reperta fue
rit alia media proportionalis propoſi-
tum obtinebimus.
ius axes ſint .a.b. et .d.c. dati, ſeu reperti ex
47. ſecundi Pergei, ſintque; duo circuli .a.e.
b.f. et .g.d.h.c. circa eaſdem diametros,
tunc proportio .a.b. ad .d.c. dimidium erit
proportionis circulorum ex .2. 12. Eu-
clid. ſed proportio .a.b. ad .d.c. æqualis
eſt proportioni maioris circuli ad Elli
pſim .ex .5. Archimedis in lib. de cono
idalibus, quapropter proportio Elli-
pſis ad minorem circulum altera me-
dietas erit totius proportionis circulo-
rum, hoc eſt maioris ad minorem, qua
re Ellipſis media proportionalis erit
inter eos circulos. Nunc verò cum
ex Archimede repertę fuerint duæ fi-
guræ rectilineæ æquales duobus circu
lis iam dictis, & inter has, reperta fue
rit alia media proportionalis propoſi-
tum obtinebimus.
Spheroidem propoſitam cubare.
AD EVNDEM.
PRopoſita ſphæroides erit, aut prolata, aut oblonga, ſit prius prolata, ſitque; .a.b.
diameter circuli, qui eam per æqualia ſecat, circa quam .a.b. vt circa axem in-
telligatur ſphæroides oblonga, cuius ſpiſſitudo ſit .d.c. axis prolatæ, cogitemus nunc
duas ſphæras .a.e.b.f. et .g.d.h.c. circa dictos axes. Vnde quatuor corpora habebi-
mus, hoc eſt duas ſphæras, & duas ſphæroides, quas probabo continuas proportio-
nales inuicem eſſe.
diameter circuli, qui eam per æqualia ſecat, circa quam .a.b. vt circa axem in-
telligatur ſphæroides oblonga, cuius ſpiſſitudo ſit .d.c. axis prolatæ, cogitemus nunc
duas ſphæras .a.e.b.f. et .g.d.h.c. circa dictos axes. Vnde quatuor corpora habebi-
mus, hoc eſt duas ſphæras, & duas ſphæroides, quas probabo continuas proportio-
nales inuicem eſſe.
Conſideremus igitur duos conos rectos, quorum .a.b. diameter ſit eorum baſium,
altitudo autem maioris, æqualis ſit ſemidiametro majori, hoc eſt medietati .a.b. al-
altitudo autem maioris, æqualis ſit ſemidiametro majori, hoc eſt medietati .a.b. al-
