Commandino, Federico - Liber de centro gravitatis solidorum

Commandino, Federico, Liber de centro gravitatis solidorum, 1565

Table of figures

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

[Figure 41]

[Figure 42]

[Figure 43]

[Figure 44]

[Figure 45]

[Figure 46]

[Figure 47]

[Figure 48]

[Figure 49]

[Figure 50]

[Figure 51]

[Figure 52]

[Figure 53]

[Figure 54]

[Figure 55]

[Figure 56]

[Figure 57]

[Figure 58]

[Figure 59]

[Figure 60]

1medis. ergo punctum ν extra priſma af poſitum, centrum
erit magnitudinis compoſitæ ex omnibus priſmatibus gzr,
r βt, tγx, xδk, kδ y, yu, us, sαh, quod fieri nullo modo po
teſt. eſt enim ex diffinitione centrum grauitatis ſolidæ figu
ræ intra ipſam poſitum, non extra. quare relinquitur, ut cen
trum grauitatis priſmatis ſit in linea Km. Rurſus bc bifa
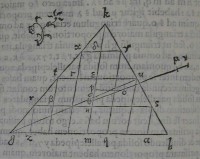
riam in diuidatur: & ducta aχ, per ipſam, & per lineam
agd planum ducatur; quod priſma ſecet: faciatque in paral
lelogrammo bf ſectionem χ π diuidet punctum π lineam
quoque cf bifariam: & erit plani eius, & trianguli ghK
communis ſectio gu; quòd punctum u in medio lineæ hK

23[Figure 23]
poſitum ſit. Similiter demonſtrabimus centrum grauita
tis priſmatis in ipſa gu ineſſe. ſit autem planorum cfnl,
adπχ communis ſectio linea ρστ; quæ quidem priſmatis
axis erit, cum tranſeat per centra grauitatis triangulorum
abc, ghk def, ex quartadecima eiuſdem. ergo centrum
grauitatis priſmatis af eſt punctum ς, centrum ſcilicet

Text layer

Text normalization

Search