1ad priſma abcefg.
quare linea sy ad yt eandem propor
tionem habet, quam priſma adcehg ad priſma abcefg.
Sed priſmatis abcefg centrum grauitatis eſt s: & priſma
tis adcehg centrum t. magnitudinis igitur ex his compo
ſitæ hoc eſt totius priſmatis ag centrum grauitatis eſt pun
ctum y; medium ſcilicet axis ux, qui oppoſitorum plano
rum centra coniungit.
tionem habet, quam priſma adcehg ad priſma abcefg.
Sed priſmatis abcefg centrum grauitatis eſt s: & priſma
tis adcehg centrum t. magnitudinis igitur ex his compo
ſitæ hoc eſt totius priſmatis ag centrum grauitatis eſt pun
ctum y; medium ſcilicet axis ux, qui oppoſitorum plano
rum centra coniungit.
5. huius/>
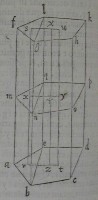
Rurſus ſit priſma baſim habens pentagonum abcde:
& quod ei opponitur ſit fghKl: ſecenturque af, bg, ch,
dk, el bifariam: & per diuiſiones ducto plano, ſectio ſit pen
tagonum mnopq. deinde iuncta eb per lineas le, eb aliud
 25[Figure 25]
25[Figure 25]
planum ducatur, diuidens priſ
ma ak in duo priſmata; in priſ
ma ſcilicet al, cuius plana op
poſita ſint triangula abe fgl:
& in prima bk cuius plana op
poſita ſint quadrilatera bcde
ghkl. Sint autem triangulo
rum abe, fgl centra grauita
tis puncta r ſ: & bcde, ghkl
quadrilaterorum centra tu:
iunganturque rs, tu occurren
tes plano mnopq in punctis
xy. & itidem iungantur rt, ſu,
xy. erit in linea rt centrum gra
uitatis pentagoni abcde;
quod ſit z: & in linea ſu cen
trum pentagoni fghkl :ſit au
tem χ· & ducatur zχ, quæ di
cto plano in ψ occurrat. Itaque
punctum x eſt centrum graui
tatis trianguli mnq, ac priſ
matis al: & y grauitatis centrum quadrilateri nopq, ac
priſmatis bk. quare y centrum erit pentagoni mnopq. &
& quod ei opponitur ſit fghKl: ſecenturque af, bg, ch,
dk, el bifariam: & per diuiſiones ducto plano, ſectio ſit pen
tagonum mnopq. deinde iuncta eb per lineas le, eb aliud
 25[Figure 25]
25[Figure 25]planum ducatur, diuidens priſ
ma ak in duo priſmata; in priſ
ma ſcilicet al, cuius plana op
poſita ſint triangula abe fgl:
& in prima bk cuius plana op
poſita ſint quadrilatera bcde
ghkl. Sint autem triangulo
rum abe, fgl centra grauita
tis puncta r ſ: & bcde, ghkl
quadrilaterorum centra tu:
iunganturque rs, tu occurren
tes plano mnopq in punctis
xy. & itidem iungantur rt, ſu,
xy. erit in linea rt centrum gra
uitatis pentagoni abcde;
quod ſit z: & in linea ſu cen
trum pentagoni fghkl :ſit au
tem χ· & ducatur zχ, quæ di
cto plano in ψ occurrat. Itaque
punctum x eſt centrum graui
tatis trianguli mnq, ac priſ
matis al: & y grauitatis centrum quadrilateri nopq, ac
priſmatis bk. quare y centrum erit pentagoni mnopq. &
