341329EPISTOL AE.
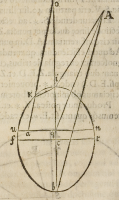
rem, quæ ita reperientur, efficiemus primo anguium coni, qui ſit .i.A.b. quem diui-
demus per æqualia mediante .A.q. conſtituendo .A.i. huius anguli æqualem .A.i. ſu-
perficiei conicæ et .A.q. diuidentem, æqualem parti .A.q. axis coni, ducendo poſtea
ab .i. per .q. lineam vnam quouſque concurrat .A.b. in puncto .b. habebimus .i.b. pro
maiori axi ipſi ellipſis, quod per ſe clarum eſt, cuius medietas ſit .i.c. ſed .i.q. ipſius .i.
b. æqualis eſt ipſi .q.i. ipſius coni, ex quarta primi Eucli. et .q.b. ipſius .i.b. æqualis alte
ri parti inuiſibili. Reliquum eſt, vt reperiamus minorem axem, quem vocabimus .
f.r. ducatur ergo primum .q.a.u.n. ad rectos cum .i.b. æqualisque; ei quæ eſt coni, & diui
ſa ſimiliter in .a. quæ .u.n. ipſius coni nobis cognita eſt ex lateribus .A.u. et .A.n. & ex
angulo coni, et .a.q. æqualis eſt .e.p. ex .34. primi. Nunc certi erimus ex .21. primi
Pergei, quod eadem proportio erit quadrati .u.q. ad quadratum ipſius .f.c. quæ pro-
ducti ipſius .i.q. in .q.b. ad productum ipſius .i.c. in .c.b. & cum cognita nobis ſint
hæc tria producta hoc eſt .i.q. in .q.b. et .i.c. in .c.b. et .u.q. in ſeipſa, cognoſcemus etiam
quartum ipſius .f.c. & fic .f.c. eiuſque; duplum .f.r. cogniti nobis itaque cum ſint hi duo
axes .i.b. et .f.r. formabimus ellipſim. Deinde producemus axim .b.i. à part e.i. quo-
uſque .i.o. æqualis ſit ei quæ extra conum eſt, dein-
364[Figure 364]
de ducemus .o.a. quæ circunferentiam ellipticam
ſecabit in puncto .K. vnde habebimus quantita-
tem ipſius .o.K. et .K.i. rectam. inde mediante cir-
cino ſi acceperimus rectam diſtantiam ab .i. ad .K.
in ellipſi, deinde firmando pedem circini in pun-
cto .i. in ſuperficie conica, & cum alio ſignando
lineam vnam curuam ad partem .K. in ſuperficie
conica, ſumendo poſtea interuallum .o.K. extra el
lipſim, deinde firmando vnum pedem circini in
extre mitate gnomonis, cum alio poſtea ſignan-
do aliam lineam curuam in ſuperficie ipſius coni,
quæ primam ſe cet in puncto .K. hoc erit punctum
quæſitum horę propoſitæ in ſuperficie conica
propoſita.
demus per æqualia mediante .A.q. conſtituendo .A.i. huius anguli æqualem .A.i. ſu-
perficiei conicæ et .A.q. diuidentem, æqualem parti .A.q. axis coni, ducendo poſtea
ab .i. per .q. lineam vnam quouſque concurrat .A.b. in puncto .b. habebimus .i.b. pro
maiori axi ipſi ellipſis, quod per ſe clarum eſt, cuius medietas ſit .i.c. ſed .i.q. ipſius .i.
b. æqualis eſt ipſi .q.i. ipſius coni, ex quarta primi Eucli. et .q.b. ipſius .i.b. æqualis alte
ri parti inuiſibili. Reliquum eſt, vt reperiamus minorem axem, quem vocabimus .
f.r. ducatur ergo primum .q.a.u.n. ad rectos cum .i.b. æqualisque; ei quæ eſt coni, & diui
ſa ſimiliter in .a. quæ .u.n. ipſius coni nobis cognita eſt ex lateribus .A.u. et .A.n. & ex
angulo coni, et .a.q. æqualis eſt .e.p. ex .34. primi. Nunc certi erimus ex .21. primi
Pergei, quod eadem proportio erit quadrati .u.q. ad quadratum ipſius .f.c. quæ pro-
ducti ipſius .i.q. in .q.b. ad productum ipſius .i.c. in .c.b. & cum cognita nobis ſint
hæc tria producta hoc eſt .i.q. in .q.b. et .i.c. in .c.b. et .u.q. in ſeipſa, cognoſcemus etiam
quartum ipſius .f.c. & fic .f.c. eiuſque; duplum .f.r. cogniti nobis itaque cum ſint hi duo
axes .i.b. et .f.r. formabimus ellipſim. Deinde producemus axim .b.i. à part e.i. quo-
uſque .i.o. æqualis ſit ei quæ extra conum eſt, dein-
ſecabit in puncto .K. vnde habebimus quantita-
tem ipſius .o.K. et .K.i. rectam. inde mediante cir-
cino ſi acceperimus rectam diſtantiam ab .i. ad .K.
in ellipſi, deinde firmando pedem circini in pun-
cto .i. in ſuperficie conica, & cum alio ſignando
lineam vnam curuam ad partem .K. in ſuperficie
conica, ſumendo poſtea interuallum .o.K. extra el
lipſim, deinde firmando vnum pedem circini in
extre mitate gnomonis, cum alio poſtea ſignan-
do aliam lineam curuam in ſuperficie ipſius coni,
quæ primam ſe cet in puncto .K. hoc erit punctum
quæſitum horę propoſitæ in ſuperficie conica
propoſita.
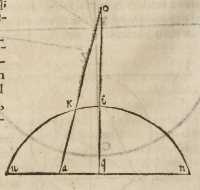
Sed ſi talis ſectio fuerit parabole, vel hyperbo
le, tunc mediante ſuo diametro .i.q. cum baſi .u.
q.n. cognita, deſignabimus ipſam ſectionem .u.i. n
ope mei inſtrumenti in calce meę gnomonicæ de
ſcripti, deinde diuiſa .u.q. in .a. productaque; q.i. vſque;
365[Figure 365]
ad .o. ductaque; .o.a. habebimus punctum .K.
Reli-
qua facienda ſunt, vt dictum eſt de ellipſi.
le, tunc mediante ſuo diametro .i.q. cum baſi .u.
q.n. cognita, deſignabimus ipſam ſectionem .u.i. n
ope mei inſtrumenti in calce meę gnomonicæ de
ſcripti, deinde diuiſa .u.q. in .a. productaque; q.i. vſque;
qua facienda ſunt, vt dictum eſt de ellipſi.
Inuenta modo cum fuerint duo puncta eiuſ-
dem horæ propoſitę, ducemus ab vno ad a-
liud, lineam horariam mediante circino trium
crurum, quem tibi ſcripſi nudius tertius pro cyl
lindro, quæ quidem linea crit portio gyri ellipſis,
ſeu hyperbolę, vel parabolę, vt à te ipſo cogi-
tare potes.
dem horæ propoſitę, ducemus ab vno ad a-
liud, lineam horariam mediante circino trium
crurum, quem tibi ſcripſi nudius tertius pro cyl
lindro, quæ quidem linea crit portio gyri ellipſis,
ſeu hyperbolę, vel parabolę, vt à te ipſo cogi-
tare potes.