PROPOSITIO XV.
Si duo gravia descendunt alterum quidem
perpendiculariter, alterum vero super pla
no declinante, perveniunt ad idem pla
num Orizontale tali ratione, ut sit eadem
proportio inter diuturnitates eorum, quae
inter perpendicularem, & declinantem.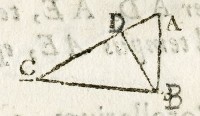 16[Figure 16]
16[Figure 16]
perpendiculariter, alterum vero super pla
no declinante, perveniunt ad idem pla
num Orizontale tali ratione, ut sit eadem
proportio inter diuturnitates eorum, quae
inter perpendicularem, & declinantem.
 16[Figure 16]
16[Figure 16]
Sit linea AB perpendiculariter erecta super
plano Orizontali BC, & AC planum declinans.
plano Orizontali BC, & AC planum declinans.
Dico quod diuturnitates gravium descendentium
per AB, & per AC, sunt ut AB ad AC.
per AB, & per AC, sunt ut AB ad AC.
Fiat AD tertia proportionalis ad AC, & AB,
Per 11. Sexti.
Quoniam est ut AD ad AC ita quadratum tem
poris AD ad quadratum temporis AC, &
tempora AD, & AB sunt aequalia, & proin
de eorum quadrata, ergo ut AD, ad AC
ita quadratum temporis AB ad quadratum
temporis AC, sed ut AD ad AC ita quadra
tum AB ad quadratum AC, ergo ut quadratum temporis AB ad quadratum temporis A
C, ita quadratum AB ad quadratum AC,
sed quia latera sunt inter se ut eorum qua
drata, est ut AB ad AC ita tempus AB ad
tempus AC. Quod, etc.
poris AD ad quadratum temporis AC, &
tempora AD, & AB sunt aequalia, & proin
de eorum quadrata, ergo ut AD, ad AC
ita quadratum temporis AB ad quadratum
temporis AC, sed ut AD ad AC ita quadra
tum AB ad quadratum AC, ergo ut quadratum temporis AB ad quadratum temporis A
C, ita quadratum AB ad quadratum AC,
sed quia latera sunt inter se ut eorum qua
drata, est ut AB ad AC ita tempus AB ad
tempus AC. Quod, etc.
Per cor. 7. huius.
Per 14. huius.
Per 2. pron.
Per 19. Sexti.
Per 11. Quinti.
Per 22. Sexti.
