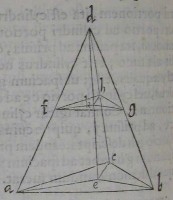
SIT pyramis, cuius baſis triangulum abc; axis dc: &
ſecetur plano baſi æquidiſtante; quod ſectionem faciat fgh;
occurratque axi in puncto k. Dico fgh triangulum eſſe, ipſi
abc ſimile; cuius grauitatis centrum eſt K. Quoniam enim
duo plana æquidiſtantia abc, fgh ſecantur à plano abd;
communes eorum ſectiones ab, fg æquidiſtantes erunt: &
eadem ratione æquidiſtantes ipſæ bc, gh: & ca, hf. Quòd
cum duæ lineæ fg, gh, duabus ab, bc æquidiſtent, nec
ſint in eodem plano; angulus ad g æqualis eſt angulo ad
b. & ſimiliter angulus ad h angulo ad c: angulusque ad fci,
qui ad a eſt æqualis. triangulum igitur fgh ſimile eſt tri
angulo abc. Atuero punctum k centrum eſſe grauita
tis trianguli fgh hoc modo oſtendemus. Ducantur pla
na per axem, & per lineas da, db, dc: erunt communes ſe
ctiones fK, ae æquidiſtantes: pariterque kg, eb; & kh, ec:
quare angulus kfh angulo eac; & angulus kfg ipſi eab
 30[Figure 30]
30[Figure 30]
eſt æqualis. Eadem ratione
anguli ad g angulis ad b: &
anguli ad h iis, qui ad c æ
quales erunt. ergo puncta
eK in triangulis abc, fgh
ſimiliter ſunt poſita, per ſe
xtam poſitionem Archime
dis in libro de centro graui
tatis planorum. Sed cum e
ſit centrum grauitatis trian
guli abc, erit ex undecima
propoſitione eiuſdem libri,
& K trianguli fgh grauita
tis centrum. id quod demonſtrare oportebat. Non aliter
in ceteris pyramidibus, quod propoſitum eſt demonſtra
bitur.
ſecetur plano baſi æquidiſtante; quod ſectionem faciat fgh;
occurratque axi in puncto k. Dico fgh triangulum eſſe, ipſi
abc ſimile; cuius grauitatis centrum eſt K. Quoniam enim
duo plana æquidiſtantia abc, fgh ſecantur à plano abd;
communes eorum ſectiones ab, fg æquidiſtantes erunt: &
eadem ratione æquidiſtantes ipſæ bc, gh: & ca, hf. Quòd
cum duæ lineæ fg, gh, duabus ab, bc æquidiſtent, nec
ſint in eodem plano; angulus ad g æqualis eſt angulo ad
b. & ſimiliter angulus ad h angulo ad c: angulusque ad fci,
qui ad a eſt æqualis. triangulum igitur fgh ſimile eſt tri
angulo abc. Atuero punctum k centrum eſſe grauita
tis trianguli fgh hoc modo oſtendemus. Ducantur pla
na per axem, & per lineas da, db, dc: erunt communes ſe
ctiones fK, ae æquidiſtantes: pariterque kg, eb; & kh, ec:
quare angulus kfh angulo eac; & angulus kfg ipſi eab
 30[Figure 30]
30[Figure 30]eſt æqualis. Eadem ratione
anguli ad g angulis ad b: &
anguli ad h iis, qui ad c æ
quales erunt. ergo puncta
eK in triangulis abc, fgh
ſimiliter ſunt poſita, per ſe
xtam poſitionem Archime
dis in libro de centro graui
tatis planorum. Sed cum e
ſit centrum grauitatis trian
guli abc, erit ex undecima
propoſitione eiuſdem libri,
& K trianguli fgh grauita
tis centrum. id quod demonſtrare oportebat. Non aliter
in ceteris pyramidibus, quod propoſitum eſt demonſtra
bitur.
