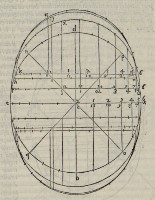
1diuiſa la quarta a b in parti nouanta, & ſiano dal punto a numerate parti uentitre & me
za, & doue terminano ſia posto f. ſiano anche numerate dal punto a parti 20, & minu
ti 12, & iui ſia fatto il punto o. & finalmente dal punto a ſiano numerate parti undici,
& meza & ſia nel termine poſto k. ſiano poi riportate quelle diſtanze f. o. k. ſotto il pun-
 126[Figure 126]
126[Figure 126]
to a, ſi che a f. ſia a
h. & a o ſia a que et
a k. ſia a m. il mede
ſimo ſi faccia nella parte
oppoſta dal punto d tan
to di ſopra quanto di ſot
to, ſi che g riſponda ad
f. p ad o. l. à K. n
ad m. r. à que & i ad
h. ſiano poi tirate le linee
f g. o p. K l. m n. q
r. h s. queſte linee ci ſer
ueno per diametri di que
circoli o giri, che fa il So
le quando egli ſi troua ne i
principij de i ſegni del Zo
diaco, di modo, che il dia
metro f g. è il diametro
di quel circolo, che fa il So
le quando egli entrà nel
Cancro, & h i. è il dia
metro del circolo del Ca
pricorno. ſi come o p. di
Gemini, & di Leone. k l
del Toro, & della Vergi
ne. m n. di Peſci & di
Scorpione, q r di Aqua
rio, & Sagittario, & que
ſte diſtanze ſono preſe dal
la declinatione del Sole, che per la tauola di detta declinatione ci ſono manifeſte. ouero per la li
nea lacotomus, & per lo circolo Monachus detti da Vitr. & per le iſteſſe uie, cioe della tauola
della declinatione del Sole, o della diuiſione del circolo detto monachus, ſi poſſono fare tutti i dia
metri di grado in grado, o di cinque in cinque, o di dieci in dieci, come piu ci piacerà, di tutti i cir
coli & giri del Sole quando egli è nelle parti de i ſegni. uero è, che per non fare confuſione di mol
te linee ci ſeruiremo di quattro diametri, cioè dell'equinottiale, del tropico uerſo il polo di ſopra,
& del diametro del Toro pure uerſo il polo, & del diametro del Saggittario di ſotto; perche la
ragione di uno ſarà la iſteſſa con la ragione dell'altro, come dirò di ſotto. ſiano adunque ſopra i
predetti diametri tirati i ſemicircoli, ſi che i centri loro ſiano la doue detti diametri tagliano l'aſ
ſe del mondo, la doue e s. ſarà il centro del ſemicircolo fatto ſopra f g. & t. ſarà il cen
tro del ſemicircolo fatto ſopra il diametro q r. & queſti ſono i circoli, & i diametri communi
ad ogni Analemma. ma perche ſono diuerſe inclinationi del cielo, però uolendo fare lo Analem
ma per una inclinatione del cielo. biſogna porui de gli altri circoli, come è il uerticale, & l'orizon
te. ilche come ſi habbia a fare dirò qui ſotto. Egli biſogna adunque ſapere la altezza del polo a
quel luogo, per loquale ſi ha da fare l'horologio, come ſe noi uogliamo fare un'horologio per ſer-
za, & doue terminano ſia posto f. ſiano anche numerate dal punto a parti 20, & minu
ti 12, & iui ſia fatto il punto o. & finalmente dal punto a ſiano numerate parti undici,
& meza & ſia nel termine poſto k. ſiano poi riportate quelle diſtanze f. o. k. ſotto il pun-
 126[Figure 126]
126[Figure 126]to a, ſi che a f. ſia a
h. & a o ſia a que et
a k. ſia a m. il mede
ſimo ſi faccia nella parte
oppoſta dal punto d tan
to di ſopra quanto di ſot
to, ſi che g riſponda ad
f. p ad o. l. à K. n
ad m. r. à que & i ad
h. ſiano poi tirate le linee
f g. o p. K l. m n. q
r. h s. queſte linee ci ſer
ueno per diametri di que
circoli o giri, che fa il So
le quando egli ſi troua ne i
principij de i ſegni del Zo
diaco, di modo, che il dia
metro f g. è il diametro
di quel circolo, che fa il So
le quando egli entrà nel
Cancro, & h i. è il dia
metro del circolo del Ca
pricorno. ſi come o p. di
Gemini, & di Leone. k l
del Toro, & della Vergi
ne. m n. di Peſci & di
Scorpione, q r di Aqua
rio, & Sagittario, & que
ſte diſtanze ſono preſe dal
la declinatione del Sole, che per la tauola di detta declinatione ci ſono manifeſte. ouero per la li
nea lacotomus, & per lo circolo Monachus detti da Vitr. & per le iſteſſe uie, cioe della tauola
della declinatione del Sole, o della diuiſione del circolo detto monachus, ſi poſſono fare tutti i dia
metri di grado in grado, o di cinque in cinque, o di dieci in dieci, come piu ci piacerà, di tutti i cir
coli & giri del Sole quando egli è nelle parti de i ſegni. uero è, che per non fare confuſione di mol
te linee ci ſeruiremo di quattro diametri, cioè dell'equinottiale, del tropico uerſo il polo di ſopra,
& del diametro del Toro pure uerſo il polo, & del diametro del Saggittario di ſotto; perche la
ragione di uno ſarà la iſteſſa con la ragione dell'altro, come dirò di ſotto. ſiano adunque ſopra i
predetti diametri tirati i ſemicircoli, ſi che i centri loro ſiano la doue detti diametri tagliano l'aſ
ſe del mondo, la doue e s. ſarà il centro del ſemicircolo fatto ſopra f g. & t. ſarà il cen
tro del ſemicircolo fatto ſopra il diametro q r. & queſti ſono i circoli, & i diametri communi
ad ogni Analemma. ma perche ſono diuerſe inclinationi del cielo, però uolendo fare lo Analem
ma per una inclinatione del cielo. biſogna porui de gli altri circoli, come è il uerticale, & l'orizon
te. ilche come ſi habbia a fare dirò qui ſotto. Egli biſogna adunque ſapere la altezza del polo a
quel luogo, per loquale ſi ha da fare l'horologio, come ſe noi uogliamo fare un'horologio per ſer-
