Baliani, Giovanni Battista - De motv natvrali gravivm solidorvm et liqvidorvm

Baliani, Giovanni Battista, De motv natvrali gravivm solidorvm et liqvidorvm

Table of figures

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

[Figure 41]

[Figure 42]

[Figure 43]

[Figure 44]

[Figure 45]

[Figure 46]

[Figure 47]

[Figure 48]

[Figure 49]

[Figure 50]

1

PROPOSITIO XXIII.

Duo gravia descendentia super planis diversa
ratione declinantibus, perveniunt ad idem
planum orizontale ea ratione, ut sit eadem
proportio inter diuturnitates, quae inter
dicta plana si ab eodem puncto ad idem
planum orizontale producta sint.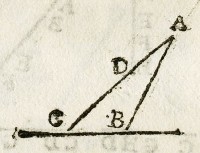

24[Figure 24]

Datis planis AB, AC declinantibus, ductis
ab eodem puncto A ad planum orizontale BC.
Dico quod diuturnitates gravium descendentium
per AB, AC sint ut AB ad AC.

Fiat ut AC ad AB ita AB ad AD, ita ut grave
perveniat in D eodem tempore quo pervenit in B.

Per 17. huius.

Quoniam est ut AD ad AC, ita quadratum tem
poris AD ad quadratum temporis AC, &
tempora AD, AB sunt aequalia, & proinde
eorum quadrata; ergo ut AD ad AC ita qua
dratum temporis AB, ad quadratum tempo
ris AC, sed ut AD ad AC, ita quadra
tum AB ad quadratum AC, ergo ut quadra
tum temporis AB ad quadratum temporis AC,
ita quadratum AB ad quadratum AC, ergo
ut tempus AB ad tempus AC, ita AB ad AC. Quod fuit probandum.

Per Cor. 7. huius.

Per const.

Per 2. pronun.

Per 10. sexti.

Per 22. sexti.

Text layer

Text normalization

Search