5442IO. BAPT. BENED.
THEOREMA LXV.
CVR propoſito numero in tres qualeſcunque partes diuiſo, ſi prima in
tertiam multiplicetur, & huic producto, ſecundæ in primam productum
coniungatur, itemque; ſecundæ in tertiam, hæc ſumma duplicata æqualis ſit ſummæ
productorum ſingularum in cæteras duas.
tertiam multiplicetur, & huic producto, ſecundæ in primam productum
coniungatur, itemque; ſecundæ in tertiam, hæc ſumma duplicata æqualis ſit ſummæ
productorum ſingularum in cæteras duas.
Exempli gratia, ſi proponatur .20. diuiſus in tres partes nempe .12. 5. 3. multipli-
cato primo .12. per .3. tertiam partem dabitur .36. ſecunda verò multiplicata per re
liquas duas, hoc eſt .5. per .12. et .3. in primis dabitur .60. poſtea .15. quorum trium pro
ductorum ſumma erit .111. quæ duplicata dabit .222. qui numerus æqualis eſſe di-
citur ſummæ productorum ſingularum partium in reliquas duas, nempe ſummæ .60.
36. 60. 15. 36. 15. hoc eſt ipſis .222.
cato primo .12. per .3. tertiam partem dabitur .36. ſecunda verò multiplicata per re
liquas duas, hoc eſt .5. per .12. et .3. in primis dabitur .60. poſtea .15. quorum trium pro
ductorum ſumma erit .111. quæ duplicata dabit .222. qui numerus æqualis eſſe di-
citur ſummæ productorum ſingularum partium in reliquas duas, nempe ſummæ .60.
36. 60. 15. 36. 15. hoc eſt ipſis .222.
Cuius rei per ſe patet ſpeculatio, cum in his ſex vltimis productis, ſingula tria
prima duplicentur.
prima duplicentur.
THEOREMA LXVI.
CVR propoſito numero in .3. qualeſcunque partes diuiſo, ſi in reliquas duas ſin-
gulæ multiplicentur, & hæc producta cum ſumma ſuorum quadratorum con-
iungantur, tota ſumma hæc vltima æqualis erit quadrato totali propoſiti numeri.
gulæ multiplicentur, & hæc producta cum ſumma ſuorum quadratorum con-
iungantur, tota ſumma hæc vltima æqualis erit quadrato totali propoſiti numeri.
Exempli gratia, ſi fuerit idem numerus .20. in .3. partes diuiſus .12. 5. 3.
Si .12. in
5. et .3. producatur, ſumma productorum erit .96. at .5. in .12. et .3. erit .75. poſtmo-
dum .3. in .12. et .5. erit .51. nempe in vniuerſum .222. quadratorum porrò ſumma
erit .178 quæ coniuncta .222. dabit .400. quadratum ipſius .20.
5. et .3. producatur, ſumma productorum erit .96. at .5. in .12. et .3. erit .75. poſtmo-
dum .3. in .12. et .5. erit .51. nempe in vniuerſum .222. quadratorum porrò ſumma
erit .178 quæ coniuncta .222. dabit .400. quadratum ipſius .20.
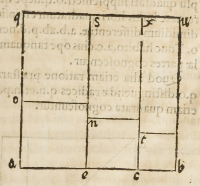
Erit autem huiuſce rei facillima ſpeculatio, ſi ſequentem figuram mente conce-
perimus, in qua .a.b. propoſitum numerum ſignificet, cuius partes diſtinctæ ſint me-
dio .e. et .c. Ip ſum autem .q.b. ſit quadratum
totale parallelis .e.s. et .c.x. diuiſum, quæ qua
74[Figure 74]
dratum in triarectangula diuident, quorum
primum erit .q.e. compoſitum ex producto .a.
e. in ſemetipſam, nempe quadratum .o.e. &
ex producto eiuſdem .a.e. in .e.b. quod erit re
ctangulum .o.s. ex quo tria rectangula .o.s. et .
n.x. et .t.u. tria producta erunt ſingularum par
tium in cæteras duas, et .e.o: c.n: b.t. tria qua-
drata erunt: quibus ſex quantitatibus quadra
tum totale .q.b. completur.
perimus, in qua .a.b. propoſitum numerum ſignificet, cuius partes diſtinctæ ſint me-
dio .e. et .c. Ip ſum autem .q.b. ſit quadratum
totale parallelis .e.s. et .c.x. diuiſum, quæ qua
primum erit .q.e. compoſitum ex producto .a.
e. in ſemetipſam, nempe quadratum .o.e. &
ex producto eiuſdem .a.e. in .e.b. quod erit re
ctangulum .o.s. ex quo tria rectangula .o.s. et .
n.x. et .t.u. tria producta erunt ſingularum par
tium in cæteras duas, et .e.o: c.n: b.t. tria qua-
drata erunt: quibus ſex quantitatibus quadra
tum totale .q.b. completur.
THEOREMA LXVII.
VEteres aliud quoque problema indefinitum propoſuerunt, quod tamen à
nobis determinabitur.
nobis determinabitur.
Cur diuiſuri propoſitum numerum in duas eiuſmodi partes, vt mutuò diuiſis, &
per ſummam prouenientium diuiſa ſumma qua dratorum partium, oriatur proue-
niens alter numerus propoſitus.
per ſummam prouenientium diuiſa ſumma qua dratorum partium, oriatur proue-
niens alter numerus propoſitus.
Propoſito deinde tertio quolibet numero diuidendo per ſingulas partes primi,
zoom in
zoom out
zoom area
full page
page width
set mark
remove mark
get reference
digilib