percipitur quomodo à naturali operatione, deſcen
ſus nempè deorſum, produci debeat operatio quædam
contraria, aſcenſus nimirum alterius partis eiuſdem
fluidi ſcilicet recedendo a centro telluris. erit igitur
operæpretium perſpicuè oſtendere veritatem præ
dictæ operationis, eamque deducere ex principijs
magis notis, & euidentibus.
Cap.
2. dę
momentis
grauium in
fluido inna
tantium.
momentis
grauium in
fluido inna
tantium.
Grauis ſuſpenſi non ex centro ſuæ grauitatis vna eius pars
ſurſum aſcendit quiæ integrum graue deorsum deſcendit.
ſurſum aſcendit quiæ integrum graue deorsum deſcendit.
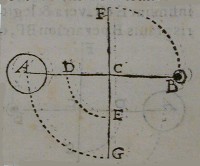
Sit graue AB extenſum, vel compoſitum ex dua
bus partibus in extremitatibus eiuſdem libræ
horizontalis AB diſpoſitis, & commune centrum gra
uitatis earum ſit D. ſuſti
 2[Figure 2]
2[Figure 2]
neatur poſtea, fulciatur
que tota libra ex puncto
C remoto à centro graui
tatis D. dico quòd pars
eius oppoſita B ſurſum̨
aſcendet per arcum BF,
hac ſolummodo de cauſą
quia integrum graue AB magis, quàm prius ad cen
trum terræ accedit. quia duæ partes graues A & B
exercent ſuam grauitatem & conatum compreſſiuum
in centro communi earum grauitatum D; eſt que
prædictum centrum D remotum à fulcimento ſtabili
C, igitur efformabitur veluti fune-pendulum CD
bus partibus in extremitatibus eiuſdem libræ
horizontalis AB diſpoſitis, & commune centrum gra
uitatis earum ſit D. ſuſti
 2[Figure 2]
2[Figure 2]neatur poſtea, fulciatur
que tota libra ex puncto
C remoto à centro graui
tatis D. dico quòd pars
eius oppoſita B ſurſum̨
aſcendet per arcum BF,
hac ſolummodo de cauſą
quia integrum graue AB magis, quàm prius ad cen
trum terræ accedit. quia duæ partes graues A & B
exercent ſuam grauitatem & conatum compreſſiuum
in centro communi earum grauitatum D; eſt que
prædictum centrum D remotum à fulcimento ſtabili
C, igitur efformabitur veluti fune-pendulum CD
