Borelli, Giovanni Alfonso - De motionibus naturalibus a gravitate pendentibus

Borelli, Giovanni Alfonso, De motionibus naturalibus a gravitate pendentibus, 1670

Table of figures

[Figure 21]

[Figure 22]

[Figure 23]

[Figure 24]

[Figure 25]

[Figure 26]

[Figure 27]

[Figure 28]

[Figure 29]

[Figure 30]

[Figure 31]

[Figure 32]

[Figure 33]

[Figure 34]

[Figure 35]

[Figure 36]

[Figure 37]

[Figure 38]

[Figure 39]

[Figure 40]

[Figure 41]

[Figure 42]

[Figure 43]

[Figure 44]

[Figure 45]

[Figure 46]

[Figure 47]

[Figure 48]

[Figure 49]

[Figure 50]

1

Cap. 2. dę
momentis
grauium in
fluido inna
tantium

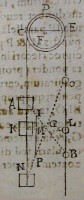
SIt pondus A maius, B verò minus alligata extre
mitatibus funis ADB, qui ſupponatur omninò
grauitate carere, & reuoluatur circa trochleam CDE
conuertibilem circa axim fixum F. patet quòd funes
AC, & BE perpendiculariter ad ho

10[Figure 10]
rizontem CE prementes, & extenſi
contingunt peripheriam rotæ in ter
minis oppoſitis C, & E eiuſdem dia
metri, ſeu libræ horizontalis, ergo
funes CA, & EB ſunt inter ſe paralle
li; coniungatur poſtea recta linea AB,
ſeceturque bifariam in G, & vt pon
dus A ad B ita fiat diſtantia BI ad IA
manifeſtum eſt (ex mechanicis) punc
tum I eſſe centrum grauitatis com
munis duorum colligatorum ponde
rum A & B, funis enim hanc propor
tionem non alterat, cùm nullius gra
uitatis ſupponatur: aſcendat poſtea
pondus minus B vbicumque ad L, & deprimatur ma
ius pondus A vſque ad K. dico quod ambo in com
muni centro grauitatis deſcendunt circa libræ cen
trum, ſeu fulcimentum ſtabile G motu directo, & per
pendiculari ad horizontem. coniungatur recta lineą
KL quia funis ADB æqualis, imò idem eſt, quàm K
DL, igitur ablato communi ADL erit deſcenſus AK
æqualis aſcenſui BL; quare in triangulis ſimilibus
ob æquidiſtantiam laterum AK & BL homologorum
vt AK ad BL ita erit AG ad GB & ita pariter KML

Text layer

Text normalization

Search