Borelli, Giovanni Alfonso - De motionibus naturalibus a gravitate pendentibus

Borelli, Giovanni Alfonso, De motionibus naturalibus a gravitate pendentibus, 1670

Table of figures

[Figure 71]

[Figure 72]

[Figure 73]

[Figure 74]

[Figure 75]

[Figure 76]

[Figure 77]

[Figure 78]

[Figure 79]

[Figure 80]

[Figure 81]

[Figure 82]

[Figure 83]

[Figure 84]

[Figure 85]

[Figure 86]

[Figure 87]

[Figure 88]

[Figure 89]

[Figure 90]

[Figure 91]

[Figure 92]

[Figure 93]

[Figure 94]

[Figure 95]

[Figure 96]

[Figure 97]

[Figure 98]

[Figure 99]

[Figure 100]

1
eiuſdem AC ſit vt XS ad V. igitur duæ antecedentes
RX, & XS ad V, ſcilicet RS ad V eamdem propor
tionem habebit quam raritas ſpecifica aggregati ex
EF, & FG ad raritatem AC, ſuntquè moles EH, &
AC æquales, ergo eorum raritates abſolutæ ſunt pro
portionales ſpecificis, ſcilicèt ſe habent vt RS ad V.
quod erat, &c.

Cap. 4. poſi
tiuam leui
tatem noņ
dari.

PROP. XCII.

Cylindrum compoſitum ex duobus cylindris inæqualitèr ra
ris transformare in cylindrum ſimilitèr excauatum,
cuius pars continens homogenea, & æqualis ſit.
vni illorum, pars verò excauata homo
genea, & æqualis ſit reliquo.

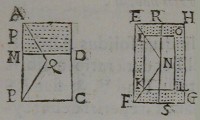
SIt datus cylindrus ſoli

73[Figure 73]
dus AC, compoſitus ex
duobus cylindris AD, & DB
inæqualitèr raris alium cy
lindrum ſimilitèr excauatum
æqualem, & ſimilem illi de
ſcribere, cuius pars continens æqualis, & homoge
nea ſit ipſi AD, contenta verò æqualis, & homoge
nea ſit ipſi DB. reperto centro que cylindricæ figuræ
AC coniungantur rectæ AQ, BQ ad terminos lateris
cylindri AB, & fiat triangulum ENF ſimile, & æqua
le ipſi AQB. poſtea inter AB, & MB reperiantur duæ
mediæ proportionales, quarum maior ſit PB (vt do
cuimus lib. 5. conic. Apoll.lemm. 7.) deinde in trian-

Text layer

Text normalization

Search