10593THEOREM. ARIT.
tum eſt, ideo cognoſcemus .e.u. ſed cum .e.u. minor ſit .a.u. ex .18. & penultima primi,
ſi demptum fuerit quadratum .e.u. ex quadrato .a.u. remanebit nobis cognitum quadra-
tum .a.e. & ſic nota erit nobis perpendicularis .a.e. ex penultima primi, quæ quidem .
a.e. ſi multiplicata fuerit in dimidium .o.u. dabit nobis ſuperficiem trianguli .a.o.u. ex
41. dicti libri. Et quia proportio trianguli .a.o.u. ad triangulum .u.i.n. (propter ſimi
litudinem) eſt vt quadrati .o.u. ad quadratum .n.i. ex communi ſcientia cum vna-
quæque iſtarum proportionum dupla ſit proportioni .o.u. ad .n.i. ex .17. et .18. ſexti,
deinde cum nobis cognitæ ſint tres iſtarum quatuor quantitatum hoc eſt ſuperficies
trianguli .a.o.u. ſuperficies trianguli .u.n.i. & quadrati .o.u. quare ex regula de tribus
cognoſcemus etiam quadratum .n.i. & ſic .n.i. latus primi trianguli, vnde reliqua la
tera illicò nobis innoteſcent exipſa regula de tribus, cum dixerimus, ſi .o.u. dat nobis
u.a. tunc .i.n. dabit .u.n. quòd etiam infero de .u.i.
ſi demptum fuerit quadratum .e.u. ex quadrato .a.u. remanebit nobis cognitum quadra-
tum .a.e. & ſic nota erit nobis perpendicularis .a.e. ex penultima primi, quæ quidem .
a.e. ſi multiplicata fuerit in dimidium .o.u. dabit nobis ſuperficiem trianguli .a.o.u. ex
41. dicti libri. Et quia proportio trianguli .a.o.u. ad triangulum .u.i.n. (propter ſimi
litudinem) eſt vt quadrati .o.u. ad quadratum .n.i. ex communi ſcientia cum vna-
quæque iſtarum proportionum dupla ſit proportioni .o.u. ad .n.i. ex .17. et .18. ſexti,
deinde cum nobis cognitæ ſint tres iſtarum quatuor quantitatum hoc eſt ſuperficies
trianguli .a.o.u. ſuperficies trianguli .u.n.i. & quadrati .o.u. quare ex regula de tribus
cognoſcemus etiam quadratum .n.i. & ſic .n.i. latus primi trianguli, vnde reliqua la
tera illicò nobis innoteſcent exipſa regula de tribus, cum dixerimus, ſi .o.u. dat nobis
u.a. tunc .i.n. dabit .u.n. quòd etiam infero de .u.i.
Poſſemus etiam ita hoc perficere,
ſcilicet inuenire .x. quantitatem me-
 144[Figure 144]
diam proportionalem inter duas ſu-
144[Figure 144]
diam proportionalem inter duas ſu-
perficies triangulorum, vnde ſuper-
ficies trianguli .i.a.u.o. ad .x. ſe ha-
beret ut .o.u. ad .i.n. & ita ex regula
detribus cognoſcemus .i.n. Multo tem
pore poſtquàm hoc theorema conſtruxi, ipſum conſcriptum inueni in decimo
ſecundi libri Ioannis de monte Regio, ſatis tamen obſcurè expreſſum.
ſcilicet inuenire .x. quantitatem me-
perficies triangulorum, vnde ſuper-
ficies trianguli .i.a.u.o. ad .x. ſe ha-
beret ut .o.u. ad .i.n. & ita ex regula
detribus cognoſcemus .i.n. Multo tem
pore poſtquàm hoc theorema conſtruxi, ipſum conſcriptum inueni in decimo
ſecundi libri Ioannis de monte Regio, ſatis tamen obſcurè expreſſum.
THEOREMA CXXXIX.
IN eodem primo libro vltimæ partis numerorum, Tartalea probat, via algebrę
quòd quælibet duo latera trianguli orthogonij, angulumrectum continentia,
ſint tertio longiora per diame-
 145[Figure 145]
trum circuli inſcriptibilis in ip-
145[Figure 145]
trum circuli inſcriptibilis in ip-
ſo triangulo. ſed hoc breuius
geometricè poteſt demonſtrari,
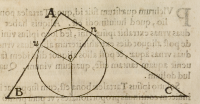
quemadmodum in ſubſcripta
hic figura videre eſt, proptereà
quòd cum anguli .A.o.u. et .n.
omnes ſint recti et .A.u. æqualis
o.n. et .A.n. ęqualis .u.o. ipſæ .A.
u. et .A.n. æquales erunt diame-
tro ipſius circuli. Sed eædem .
A.u. et .A.n. ſunt ſuperfluum, quo .A.B. et .A.C. ſunt maiores .B.C. cum .B.u. et .C.n.
ſint æquales .B.C. ex penultima tertij Eucli.
quòd quælibet duo latera trianguli orthogonij, angulumrectum continentia,
ſint tertio longiora per diame-
ſo triangulo. ſed hoc breuius
geometricè poteſt demonſtrari,
quemadmodum in ſubſcripta
hic figura videre eſt, proptereà
quòd cum anguli .A.o.u. et .n.
omnes ſint recti et .A.u. æqualis
o.n. et .A.n. ęqualis .u.o. ipſæ .A.
u. et .A.n. æquales erunt diame-
tro ipſius circuli. Sed eædem .
A.u. et .A.n. ſunt ſuperfluum, quo .A.B. et .A.C. ſunt maiores .B.C. cum .B.u. et .C.n.
ſint æquales .B.C. ex penultima tertij Eucli.
THEO. SEQVENS THEO. CXXXIX.
SImiliter in nono capite ſecundi libri nouæ ſcientiæ poterat ipſe Tartalea breuio
ri methodo abſque vlla operatione ipſius Algebræ inuenire .A.H. reſpectu .A.
E. eſſe vt .4. cum vno ſeptimo ad vnum. Nam ipſe ſupponit .A.E. decimam partem eſſe ipſius
ri methodo abſque vlla operatione ipſius Algebræ inuenire .A.H. reſpectu .A.
E. eſſe vt .4. cum vno ſeptimo ad vnum. Nam ipſe ſupponit .A.E. decimam partem eſſe ipſius
