112100IO. BAPT. BENED.
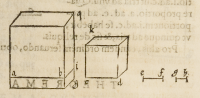
a.b: c.d: e.f. et .g.h. quorum .a.b. et .g.h. nobis tantummodo cogniti ſint, ſitque imagina
tione deſcriptus cubus .a.q. primi termini, cubusque .d.k. ſecundi rermini, conſidere-
mus etiam baſim .a.i. quadratam ipſius cubi .a.q. hoc eſt præcedentem dignitatem ip
ſius cubi eiuſdem radicis, quæ quidem baſis .a.i. multiplicetur per quartum terminum
g.h. productum autem ſit .g.a. vnde eadem proportio erit .a.q. ad .a.g. quæ .b.q. ad .b.
g. per .25. vndecimi, ſed per primam ſexti, vel .18. aut .19. ſeptimi ita eſt .q.i. ad .i.g.
vt .b.q. ad .b.g. quare per .11. quinti
ita erit .a.q. ad .a.g. vt .q.i. ad .i.g. ideſt
 155[Figure 155]
vt .a.b. ad .g.h. ſed vt eſt .a.b. ad .g.h.
155[Figure 155]
vt .a.b. ad .g.h. ſed vt eſt .a.b. ad .g.h.
ſic eſt .a.q. ad .k.d. per .36. vndecimi,
ſeu per .11. octaui, vnde per .11. quin
ti ſic erit .a.q. ad .a.g. vt ad .k.d. Qua-
re per .9. eiuſdem .a.g. ęqualis erit .k.
d. Vnde rectè erit accipere radicem
cubam .a.g. pro ſecundo termino .c.d.
id, quod nobis inſeruit ad inueniendam tertiam partem vnius propoſitæ propor-
tionis.
tione deſcriptus cubus .a.q. primi termini, cubusque .d.k. ſecundi rermini, conſidere-
mus etiam baſim .a.i. quadratam ipſius cubi .a.q. hoc eſt præcedentem dignitatem ip
ſius cubi eiuſdem radicis, quæ quidem baſis .a.i. multiplicetur per quartum terminum
g.h. productum autem ſit .g.a. vnde eadem proportio erit .a.q. ad .a.g. quæ .b.q. ad .b.
g. per .25. vndecimi, ſed per primam ſexti, vel .18. aut .19. ſeptimi ita eſt .q.i. ad .i.g.
vt .b.q. ad .b.g. quare per .11. quinti
ita erit .a.q. ad .a.g. vt .q.i. ad .i.g. ideſt
ſic eſt .a.q. ad .k.d. per .36. vndecimi,
ſeu per .11. octaui, vnde per .11. quin
ti ſic erit .a.q. ad .a.g. vt ad .k.d. Qua-
re per .9. eiuſdem .a.g. ęqualis erit .k.
d. Vnde rectè erit accipere radicem
cubam .a.g. pro ſecundo termino .c.d.
id, quod nobis inſeruit ad inueniendam tertiam partem vnius propoſitæ propor-
tionis.
THEOREMA CL.
Sed vt ſpeculatio iſta ita vniuerſalis fiat vt ad oens dignitates applicari poſſit;
Supponamus .a.q. et .k.d. eſſe duas dignitates quas volueris vnius, ſed eiuſdem
ſpeciei, et .a.i. dignitas præcedens dignitatem .a.q.a. cuius multiplicatione in .a.b.
eius radix producitur dignitas .a.q. & ab ipſius .a.i. multiplicatione in .g.h. reſultet .a.
g. vnde ex .18. vel .19. ſeptimi eadem proportio erit .a.q. ad .a.g. quæ .a.b. ad .g.h. ſed
eadem etiam eſt .a.q. ad .k.d. ex ijs, quæ in .17. theoremare dixi, vnde ex .11. quinti,
ita erit .a.q. ad .a.g. vt ad .k.d. Quapropter .a.g. æqualis erit .k.d. & ideo cum inuenta
fuerit radix huiuſmodi dignitatis ex quantitate .a.g. habebimus .c.d. ſecundum ter-
minum quæſitum.
Supponamus .a.q. et .k.d. eſſe duas dignitates quas volueris vnius, ſed eiuſdem
ſpeciei, et .a.i. dignitas præcedens dignitatem .a.q.a. cuius multiplicatione in .a.b.
eius radix producitur dignitas .a.q. & ab ipſius .a.i. multiplicatione in .g.h. reſultet .a.
g. vnde ex .18. vel .19. ſeptimi eadem proportio erit .a.q. ad .a.g. quæ .a.b. ad .g.h. ſed
eadem etiam eſt .a.q. ad .k.d. ex ijs, quæ in .17. theoremare dixi, vnde ex .11. quinti,
ita erit .a.q. ad .a.g. vt ad .k.d. Quapropter .a.g. æqualis erit .k.d. & ideo cum inuenta
fuerit radix huiuſmodi dignitatis ex quantitate .a.g. habebimus .c.d. ſecundum ter-
minum quæſitum.
THEOREMA CLI.
Vnde verò fiat, quòd cum quis voluerit dimidium alicuius datæ proportio-
nis inuenire, rectè faciat, ſi accipiat radices quadratas illorum datorum rer-
minorum, etſi voluerit tertiam partem, accipiat radices cubas: ſi autem quartam,
accipereradices cenſicas cenſicas ipſorum, & ſic de ſingulis in .17. Theoremate om-
nia patent.
nis inuenire, rectè faciat, ſi accipiat radices quadratas illorum datorum rer-
minorum, etſi voluerit tertiam partem, accipiat radices cubas: ſi autem quartam,
accipereradices cenſicas cenſicas ipſorum, & ſic de ſingulis in .17. Theoremate om-
nia patent.
THEOREMA CLII.
Vnde autem fiat, vt cum quis voluerit multiplicare aliquam proportionem
per fractos, rectè faciat prius multiplicando eam per numeratorem, dein-
de productum diuiſerit per denominationem ipſorum fractorum.
per fractos, rectè faciat prius multiplicando eam per numeratorem, dein-
de productum diuiſerit per denominationem ipſorum fractorum.
Vt exempli gratia, cum aliquis voluerit multiplicare proportionem ſeſquiquar-
tam per duo tertia, multiplicabit prius ipſam proportionem per numeratorem .2.
& productum, erit proportio .25. ad .16. qua poſtea diuiſa per .3. denominatorem,
prouentus erit proportio radicis cubæ .25. ad radicem cubam .16. vel vt proportio.
tam per duo tertia, multiplicabit prius ipſam proportionem per numeratorem .2.
& productum, erit proportio .25. ad .16. qua poſtea diuiſa per .3. denominatorem,
prouentus erit proportio radicis cubæ .25. ad radicem cubam .16. vel vt proportio.
