Benedetti, Giovanni Battista de - Io. Baptistae Benedicti ... Diversarvm specvlationvm mathematicarum, et physicarum liber : quarum seriem sequens pagina indicabit ; [annotated and critiqued by Guidobaldo Del Monte]

Scan	Original
91	79
92	80
93	81
94	82
95	89
96	84
97	85
98	96
99	87
100	88
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108

120108IO. BAPT. BENED.

Diſponantur igitur huiuſmo-

163[Figure 163] di numeri tali ordine, vt fim-
plex ſumma, quæ ab vna reli-
quarum ſuperatur, & aliam ſupe-
rat, medium locum teneat; @t
in propoſito exemplo ſumma
mediocris eft .48. quę à ſumma .
60. ſuperatur, & ſuperat ſum-
mam .39. locata igitur fit hęc .48.
inter illas, ſuæ verò primæ partes
fimiliter conftitutæ ſint ſupra di-
ctas ſummas, cum ſuis differentijs,
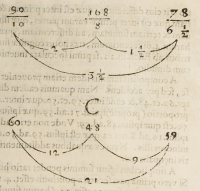
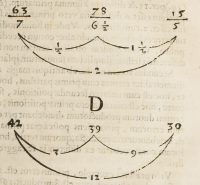
& tria producta iam dicta, vt in fi
guris .C. et .D. arithmeticis
clarè patet: figura enim .C. eft
pro exemplo ipſius plus ſimpli-
citer: figura verò .D. pro exem-
plo ipſius plus, & minus. Et fic

164[Figure 164] in figura .C. habebimus tres
numeros confequentes .60. 48.
39. & tres antecedentes .10. 8.
6. cum dimidio, vnam, & ean-
dem proportionem terminantes,
ex .24. quinti, vt diximus; qua-
re eorum differentiæ fimiliter
proportionales erunt, quod etiam
vidimus. Supponamus nunc nos
ignorare æqualitatem maximi
producti cum reliquis duobus,
accipiendo ſolum pro hypoteſi,
quòd dicta producta oriantur
ex lateribus iam dictis.

Demonſtrandum nobis nunc relinquetur, maximum productum æquale effere-
liquis duobus; hoc eſt productum .168. æquale effe productis .90. et .78. quorum
duorum productorum alterum .90. ſcilicet, generatur à differentia .9. quæ eft ſe-
cundę, & tertię ſummæ, in primum numerum antecedentem, qui eſt .10. alterum vc-
ro productum .78. ſcilicet, generatur à differentia .12. quę eſt primę, & ſecundę, ſum
mę in tertium numerum antecedentem, qui eſt .6. cum dimidio, maximum vero
productum .168. ſcilicet generatur à differentia maxima .21. quę eft primę, & tertię
ſummę (& ſemper ęqualis prioribus duabus differentijs .12. et .9.) in ſecundum nu-
merum antecedentem, qui eſt .8.

Conſtituantur igitur duo producta fimul iuncta ęqualia duobus .90. et .78.
lateralibus ſupra vnam aliquam rectam lineam .q.p. fitque; productum .f.g. ęquale .
90. productum verò .g.n. ęquale .78. fit etiam baſis .g.p. vt .9. et .g.q. vt .12. vnde .g.i.
vel .q.n. erit vt .6. cum dimidio .et .g.d. vel .p.f. vt .10. & ideo .i.d. differentia erit .3.

Page concordance

Text layer

Text normalization

Search

Scan	Original
91	79
92	80
93	81
94	82
95	89
96	84
97	85
98	96
99	87
100	88
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108

Scan	Original
91	79
92	80
93	81
94	82
95	89
96	84
97	85
98	96
99	87
100	88
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108

Scan	Original
91	79
92	80
93	81
94	82
95	89
96	84
97	85
98	96
99	87
100	88
101	89
102	90
103	91
104	92
105	93
106	94
107	95
108	96
109	97
110	98
111	99
112	100
113	101
114	102
115	103
116	104
117	105
118	106
119	107
120	108