307295EPISTOL AE.
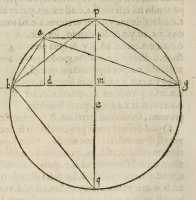
Propoſitum ſit nobis triangulum .a.b.g. cuius baſis data ſit cum area, ſeu perpendi-
culari .a.d. cum angulo etiam .a. ad cognoſcendum autem .a.b. et .b.g. cogitemus circu
lum .a.b.q.g. circunſcribere ipſum triangulum cuius diameter .p.q. ad rectos ſe-
cet baſim .b.g. in puncto .m. cogitemus etiam .b.p. et .p.g. vnde ex .20. ter-
tij Euclid. angulus .b.p.g. æqualis erit
 330[Figure 330]
angulo .a. & angulus .m.p.b. erit eius di
330[Figure 330]
angulo .a. & angulus .m.p.b. erit eius di
midium, quod ex te ipſo cognoſces, &
angulus .p.b.m. ſimiliter cognoſcetur,
quare ex .29. primi eiuſdem Montere
gij cognoſcemus .p.m. et .p.b. (nam .b.
m. datum fuit, vt dimidium totius ba-
ſis .b.g.) ducta poſtea .b.q. ex eadem .29.
cognoſcemus .p.q. cum .p.b. iam cogni
ta fuerit, à qua .p.q. (diametro) dempta
p.m. remanebit .q.m. cognita, cum qua
iuncta cum fuerit .m.t. æquali .a.d. per
pendiculari, dabitur .q.t. et .t.p. inter
quas .a.t. media proportionalis loca-
tur, quare cognoſcemus .a.t. quæ ſinus
eſt arcus .a.p. vnde cognitus erit arcus
a.p. ſed arcus .p.g. cognitus eſt median
te angulo .p.b.g. cognito, qui quidem
arcus .p.g. ſi coniunctus fuerit cum arcu .p.a. cognoſcemus compoſitum .a.g. & eius
chorda ſimiliter (hoc eſt ſecundum latus) qua cognita, illico cognoſcemus chordam
a.b. hoc eſt tertium latus trianguli propoſiti.
culari .a.d. cum angulo etiam .a. ad cognoſcendum autem .a.b. et .b.g. cogitemus circu
lum .a.b.q.g. circunſcribere ipſum triangulum cuius diameter .p.q. ad rectos ſe-
cet baſim .b.g. in puncto .m. cogitemus etiam .b.p. et .p.g. vnde ex .20. ter-
tij Euclid. angulus .b.p.g. æqualis erit
midium, quod ex te ipſo cognoſces, &
angulus .p.b.m. ſimiliter cognoſcetur,
quare ex .29. primi eiuſdem Montere
gij cognoſcemus .p.m. et .p.b. (nam .b.
m. datum fuit, vt dimidium totius ba-
ſis .b.g.) ducta poſtea .b.q. ex eadem .29.
cognoſcemus .p.q. cum .p.b. iam cogni
ta fuerit, à qua .p.q. (diametro) dempta
p.m. remanebit .q.m. cognita, cum qua
iuncta cum fuerit .m.t. æquali .a.d. per
pendiculari, dabitur .q.t. et .t.p. inter
quas .a.t. media proportionalis loca-
tur, quare cognoſcemus .a.t. quæ ſinus
eſt arcus .a.p. vnde cognitus erit arcus
a.p. ſed arcus .p.g. cognitus eſt median
te angulo .p.b.g. cognito, qui quidem
arcus .p.g. ſi coniunctus fuerit cum arcu .p.a. cognoſcemus compoſitum .a.g. & eius
chorda ſimiliter (hoc eſt ſecundum latus) qua cognita, illico cognoſcemus chordam
a.b. hoc eſt tertium latus trianguli propoſiti.
Quædam not and a in Federicum Comandinum.
AD EVNDEM.
PVtabas enim me ioco dixiſſe Federicum Comandinum non omnino irrepræ-
henſibilem eſſe, vide igitur, quod ſcribit in quinto lemmate in decimam
propoſitionem libr .2. de inſidentibus aquæ Archimedis, volens demonſtra-
re eandem eſſe proportionem .l.b. ad .b.m. quæ .c.e. ad .e.a. vbi eſt aliquo modo pro-
lixum, mediante linea .c.p. cum ſuis partibus, citans etiam antecedens lemma extra
propoſitum, eo quod nec in antecedente lemmate, nec in alio, ipſe vnquam proba
uerit proportionem .c.d. ad .d.q. eſſe, vt .l.b. @d.b.m. ſed ne putes me falli, tibi demon
ſtrabo non eſſe neceſſarium ducere lineam .c.m.p. vel .q.p. eo quod cum per quintam
lib. de quadratura parabolę Archimedis, ita ſit .c.d. ad .d.e. vt .l.b. ad .b.m. exiſtente
a.c. dupla ipſi .d.c. et .e.c. dupla ipſi .g.c. et .l.d. dupla ipſi .l.b: erit, primo componen-
do .c.e. ad .e.d. vt .l.d. ad .d.m. & per æqualitatem proportionum, ita erit .e.g. ad .e.d.
vt .b.d. 2d.d.m. & per .19. quinti Eucli. ita erit .e.g. ideſt .g.c. ad .g.d. vt .b.d. ideſt .l.b.
ad .b.m. ſed .c.g. ad .g.d. eft vt .c.e. ad .e.a. ratio eſt, quia componendo ita eſt .c.d. ad .d.
g. vt .c.a. ad .a.e. & hoc eſt, quia permutando, ita eſt .a.c. ad .d.c. vt .a.e. ad .d.g. & hoc
verum eſt ex .19. quinti eo quod totius .a.c. ad totum .d.c. eft vt abſciſſi .e.c. ad abſciſ
ſum .g.c. vt ſupradixi.
henſibilem eſſe, vide igitur, quod ſcribit in quinto lemmate in decimam
propoſitionem libr .2. de inſidentibus aquæ Archimedis, volens demonſtra-
re eandem eſſe proportionem .l.b. ad .b.m. quæ .c.e. ad .e.a. vbi eſt aliquo modo pro-
lixum, mediante linea .c.p. cum ſuis partibus, citans etiam antecedens lemma extra
propoſitum, eo quod nec in antecedente lemmate, nec in alio, ipſe vnquam proba
uerit proportionem .c.d. ad .d.q. eſſe, vt .l.b. @d.b.m. ſed ne putes me falli, tibi demon
ſtrabo non eſſe neceſſarium ducere lineam .c.m.p. vel .q.p. eo quod cum per quintam
lib. de quadratura parabolę Archimedis, ita ſit .c.d. ad .d.e. vt .l.b. ad .b.m. exiſtente
a.c. dupla ipſi .d.c. et .e.c. dupla ipſi .g.c. et .l.d. dupla ipſi .l.b: erit, primo componen-
do .c.e. ad .e.d. vt .l.d. ad .d.m. & per æqualitatem proportionum, ita erit .e.g. ad .e.d.
vt .b.d. 2d.d.m. & per .19. quinti Eucli. ita erit .e.g. ideſt .g.c. ad .g.d. vt .b.d. ideſt .l.b.
ad .b.m. ſed .c.g. ad .g.d. eft vt .c.e. ad .e.a. ratio eſt, quia componendo ita eſt .c.d. ad .d.
g. vt .c.a. ad .a.e. & hoc eſt, quia permutando, ita eſt .a.c. ad .d.c. vt .a.e. ad .d.g. & hoc
verum eſt ex .19. quinti eo quod totius .a.c. ad totum .d.c. eft vt abſciſſi .e.c. ad abſciſ
ſum .g.c. vt ſupradixi.
