345333EPISTOL AE.
Si autem res viſibilis oculusque; ambo fuerint intra circulum, tunc poſſibile eſſet quod
longitudo .u.b.n. modo maior, modo minor, modo verò æqualis eſſet ipſa .u.o.n. nunc.
Quod etiam affirmo de .u.b.p. ſimiliter etiam eueniet ſi vnus terminorum .u. vel .n.
fuerit intra circunferentiam, reliquus verò extra ipſam.
longitudo .u.b.n. modo maior, modo minor, modo verò æqualis eſſet ipſa .u.o.n. nunc.
Quod etiam affirmo de .u.b.p. ſimiliter etiam eueniet ſi vnus terminorum .u. vel .n.
fuerit intra circunferentiam, reliquus verò extra ipſam.
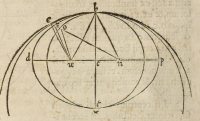
Conſideremus nunc hic inſraſcriptam .4. figuram vbi .d.b.p. ſit circunferentia oxy
gonia ſeu elliptica (quod idem eſt) cuius maior axis ſit .d.p. in quo, duo termini .u.n.
ſint centra eius generationis: b.x. verò ſit minor axis. Imaginemur etiam circulum .
b.o.x. cuius ſemidiameter ſit .c.b. non maior medietate minoris axis, ne circunferen-
tia huiuſmodi circuli ſecet circunferentiam oxygoniam. Cogitemus etiam circu-
lum .b.e. cuius ſemidiameter, minor non ſit minori axe .b.x. ipſius oxygoniæ, ne ſe
inuicem ſecent huiuſmodi circunferentiæ, ſint etiam ambo eorum centra in linea .b.
x. minoris axis, & punctum .b. ſit commune vnicuique earum periphæriarum, vnde
minor circulus, totus intra, maior autem, totus extra ipſam figuram oxygoniam erit.
Nunc ad partem .o.r.e. vbi non communicant inuicem ipſæ circunferentiæ ducan-
tur .n.o.r.e: u.o: u.r: et .u.e. & per .b. et .r. cogitetur tranſire alium circulum, cuius cen-
trum in axe .b.x. ſit .t. omnesque; iſti circuli imaginentur trium diuerſorum ſphærico-
rum ſpeculorum, vnde pro genera
tione ipſius oxygonię, ſeu ex .52. ter
tij Pergei, habebis longitudinem .
 371[Figure 371]
u.r.n. ęqualem eſſe longitudini .u.b.
371[Figure 371]
u.r.n. ęqualem eſſe longitudini .u.b.
n. & ei, quæ eſt .u.o.n. (vt minor ip
ſa .u.r.n. ex .21. primi Euclidis) mi-
nor ipſa .u.b.n. & longitudinem .u.
e.n. (vt maior ipſa .u.r.n. ex eadem .
21. primi Eucli.) maior ipſa .u.b.n.
Sed ſi quis vellet hoc demonſtrare
ope circuli, vnius tantummodo ſpeculi,
multiplicando ipſas oxygonias quem-
admodum de ipſis circulis fecimus, obtineret ſimiliter propoſitum.
gonia ſeu elliptica (quod idem eſt) cuius maior axis ſit .d.p. in quo, duo termini .u.n.
ſint centra eius generationis: b.x. verò ſit minor axis. Imaginemur etiam circulum .
b.o.x. cuius ſemidiameter ſit .c.b. non maior medietate minoris axis, ne circunferen-
tia huiuſmodi circuli ſecet circunferentiam oxygoniam. Cogitemus etiam circu-
lum .b.e. cuius ſemidiameter, minor non ſit minori axe .b.x. ipſius oxygoniæ, ne ſe
inuicem ſecent huiuſmodi circunferentiæ, ſint etiam ambo eorum centra in linea .b.
x. minoris axis, & punctum .b. ſit commune vnicuique earum periphæriarum, vnde
minor circulus, totus intra, maior autem, totus extra ipſam figuram oxygoniam erit.
Nunc ad partem .o.r.e. vbi non communicant inuicem ipſæ circunferentiæ ducan-
tur .n.o.r.e: u.o: u.r: et .u.e. & per .b. et .r. cogitetur tranſire alium circulum, cuius cen-
trum in axe .b.x. ſit .t. omnesque; iſti circuli imaginentur trium diuerſorum ſphærico-
rum ſpeculorum, vnde pro genera
tione ipſius oxygonię, ſeu ex .52. ter
tij Pergei, habebis longitudinem .
n. & ei, quæ eſt .u.o.n. (vt minor ip
ſa .u.r.n. ex .21. primi Euclidis) mi-
nor ipſa .u.b.n. & longitudinem .u.
e.n. (vt maior ipſa .u.r.n. ex eadem .
21. primi Eucli.) maior ipſa .u.b.n.
Sed ſi quis vellet hoc demonſtrare
ope circuli, vnius tantummodo ſpeculi,
multiplicando ipſas oxygonias quem-
admodum de ipſis circulis fecimus, obtineret ſimiliter propoſitum.
Solutio dubitationis.
AD EVNDEM.
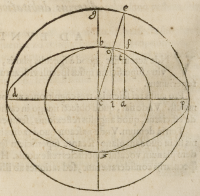
RAtionalis eſt dubitatio tua,
 372[Figure 372]
vtrum (cum circulus minor hoc
372[Figure 372]
vtrum (cum circulus minor hoc
eſt .b.o. habeat ſuum centrum in mi
nori axe inter centrum oxygoniæ,
et .b: exiſtente .b. extremo axis mi-
noris, communeque; ambobus circun-
ferentijs circuli ſcilicet & oxigonię)
dictus circulus minor, plura puncta
communia habeat cum ipſis circun-
ferentijs.
eſt .b.o. habeat ſuum centrum in mi
nori axe inter centrum oxygoniæ,
et .b: exiſtente .b. extremo axis mi-
noris, communeque; ambobus circun-
ferentijs circuli ſcilicet & oxigonię)
dictus circulus minor, plura puncta
communia habeat cum ipſis circun-
ferentijs.
Cui dubitationi reſpondeo quod
quotieſcunque centrum alicuius cir
culi fuerit idem cum .c. centro oxy-
goniæ, vel inter .c. et .b. in interual-
lo ſcilicet minoris axis, exiſtente .b.
ſua extremitate communi ambabus
quotieſcunque centrum alicuius cir
culi fuerit idem cum .c. centro oxy-
goniæ, vel inter .c. et .b. in interual-
lo ſcilicet minoris axis, exiſtente .b.
ſua extremitate communi ambabus
