Benedetti, Giovanni Battista de - Io. Baptistae Benedicti ... Diversarvm specvlationvm mathematicarum, et physicarum liber : quarum seriem sequens pagina indicabit ; [annotated and critiqued by Guidobaldo Del Monte]

Scan	Original
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70

5543THEOREM. ARIT. ita vt ſimul prouenientibus in ſummam collectis huius fummæ ad primum nume-
rum propoſitum proportio futura ſit ea quæ eſt tertij ad ſecundum. Rectè dimidium
primi numeri in ſeipſum multiplicant, ex quo quadrato ſecundum numerum detra
hunt, tum reſidui radicem ſumunt, quam iungentes, & detrahentes ex dimidio
primi, partes quæſitas habent, cætera ex neceſsitate ſubſequuntur, prout nunc a
me docebitur.

Exempli gratia, proponitur numerus .20. in duas partes diuidendus, quibus po
ſtea mutuò diuiſis, & per ſummam prouenientium diuiſa ſumma quadratorum,
dent ſecundum numerum propoſitum .36. nam reliqua conſequuntur. Itaque .10.
dimidium primi in ſeipſum multiplicatur, & ex quadrato .100. eruitur numerus .36.
nempe ſecundus propoſitus reſidui porrò .64. quadrata radix .8. fumitur, quam con
iungimus & detrahimus ex dimidio primi ſcilicet .10. ex quo partes quæſitæ dabun
tur .18. et .2. quæ mutuo diuiſæ dabunt ſuorum prouenientium ſummam .9. cum no-
na parte, per quam diuidentes .328. ſummam quadratorum ipſarum partium,
exactè dabitur numerus .36. qui fuit ſecundò propoſitus. Tum ſi per ſingu-
las iam inuentas partes quilibet numerus diuiſus fuerit, verbi gratia .72. ſumma pro
uenientium erit .40. qui num@rus eandem proportionem cum primo nempe .20. ſer
uabit, quam tertius propoſitus .72. cum ſecundo .36.

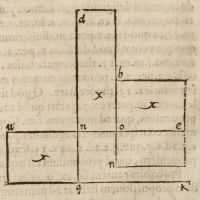
Quod vt ſpeculemur, primus numerus ſignificetur linea .n.e. ita diuidendus à
puncto .o. vt diuiſa parte .n.o. per .o.e. et .o.e. per .n.o. & per ſummam prouenien-
tium diuiſa ſumma quadratorum .n.o. et .o.e. detur ſecundus numerus notatus linea .
q.K. Porrò meminiſſe oportet quòd .26. theoremate probatum fuit vltimum hoc
proueniens æquale producto partium inter ſe futurum, nempe producto .n.o. in .o.
e. quod ſignificetur rectangulo .n.e. Itaque datis .n.e. et .q.K. ſi .45. theorema conſu-
luerimus, partes .n.o. et .o.e. cognoſcemus.

Proponitur deinde tertius quilibetnumerus, verbi gratia .x. diuidendus per .o.e.
et .o.n. qui ſi diuidatur per .o.e. dabit pro
ueniens .b.o. Si verò per .n.o. proueniens

75[Figure 75] erit .d.n. nunc aſſerimus ſummam duorum
horum prouenientium, ſic primo nume-
ro .n.e. dato proportionatam eſſe, ſicut
tertius .x. ſecundo .q.K. Producatur enim li-
nea .d.n. donec .n.q. æqualis ſit .o.b. ex
quo .q.d. erit ſumma vltimò prouenien-
tium: item producatur .e.n. donec .n.u. æ-
qualis ſit .o.e. termineturque rectangulum .
q.u. quod tertio numero propoſito .x. vt
patet, æquale erit, quare ex .15. ſexti aut .
20. ſeptimi eadem erit proportio .d.n. ad
n.q. quæ .u.n. nempe .o.e. ad .o.n. & com-
ponendo .d.q. ad .q.n. ſicut .e.n. ad .n.o. &
permutando .d.q. ad .e.n. quæ .q.n. hoc eſt .
b.o. ad .o.n. nempe ſicut .b.e. ad .e.n. ſuperficialem, ex prima ſexti aut .18. vel .19.
ſeptimi, ſed rectangulum .e.n. conſtitutum fuit æquale numero .q.K. itaque verum
eſt propoſitum.

Page concordance

Text layer

Text normalization

Search

Scan	Original
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70

Scan	Original
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70

Scan	Original
51	39
52	40
53	41
54	42
55	43
56	44
57	45
58	46
59	47
60	48
61	49
62	50
63	51
64	52
65	53
66	54
67	55
68	56
69	57
70	58
71	59
72	60
73	61
74	62
75	63
76	64
77	65
78	66
79	67
80	70