122110IO. BAPT. BENED.
DEmpto poſteà quo volueris horum altero productorum ex maximo, diuiſoque;
reliquo per differentiam conſequentium, ipſi diametraliter oppoſitam, pro
ueniet tibi numerus antecedens correſpondensque; illi.
reliquo per differentiam conſequentium, ipſi diametraliter oppoſitam, pro
ueniet tibi numerus antecedens correſpondensque; illi.
Animaduertendum tamen eſt, quòd ſi in figura à me ita ordinata, ſumma ſim-
plex propoſita medium locum occuparet, vt in figura .D. arithmetica videri poteſt;
tunc vt habeatur eius productum, addenda ſimul erunt circunſtantia producta .eo
quod eius ſecundum latus eſſet antecedens medio loco conſtitutum, & prima pars quae-
ſita numeri propoſiti: in qua figura .D. manifeſtè patet ratio, quare colligendi ſint
tam errores, quam producta, dum eorum alterum eſt plus, reliquum verò minus.
plex propoſita medium locum occuparet, vt in figura .D. arithmetica videri poteſt;
tunc vt habeatur eius productum, addenda ſimul erunt circunſtantia producta .eo
quod eius ſecundum latus eſſet antecedens medio loco conſtitutum, & prima pars quae-
ſita numeri propoſiti: in qua figura .D. manifeſtè patet ratio, quare colligendi ſint
tam errores, quam producta, dum eorum alterum eſt plus, reliquum verò minus.
Speculatio figurę .D. arithmeticę videbitur in figura .D. geometrica, eodem fe
rè modo quo fecimus in figuris .C. mutatis mutandis, reſpectu ipſius plus, & minus.
rè modo quo fecimus in figuris .C. mutatis mutandis, reſpectu ipſius plus, & minus.
Collectio namque errorum ſimiliter accidentalis eſt, eo quod eſſentialis numerus
diuiſor per ſe, eſt maxima differentia ſummarum ſimplicium, vt in dicta figura .D.
cerni poteſt.
diuiſor per ſe, eſt maxima differentia ſummarum ſimplicium, vt in dicta figura .D.
cerni poteſt.
Sed vt ſuperius dixi, nunc etiam repeto, quòd rectè hoc loco multiplicabatur
ſumma ſimplex propoſita, cum prima par
te primę poſitionis, vt productum diuide
retur per primam ſimplicem ſummam,
 167[Figure 167]
vnde proueniret nobis pars prima quaeſi-
167[Figure 167]
vnde proueniret nobis pars prima quaeſi-
ta noſtri numeri propoſiti, ex regula de
tribus, vnica poſitione.
ſumma ſimplex propoſita, cum prima par
te primę poſitionis, vt productum diuide
retur per primam ſimplicem ſummam,
ta noſtri numeri propoſiti, ex regula de
tribus, vnica poſitione.
Vt exempli gratia, datus numerus diui
dendus ſit .100. in quinque partes, tales
verò, quod ſecunda duplo maior ſit prima
cum .2. ſimul, tertia autem æqualis ſit pri-
mæ & ſecundæ cum .3. vnitatibus iunctis,
quarta poſteà maior ſit prima ſecunda, &
tertia per .4. vnitates, quinta demum ſu-
peret reliquas omnes per quinque vnita
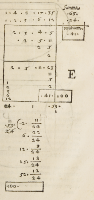
tes, vt in figura .E. videre eſt, quæ quidem
partes compoſitæ (ſumpta vnitate pro
prima) ita diſpoſitæ erunt .1. 4. 8. 17. 35.
quarum ſumma erit .65. ſimplices autem
cum diſpoſitæ fuerint erunt .1. 2. 3. 6. 12.
quarum ſumma erit .24. dempta igitur
cum fuerit hæc ſimplex ſumma .24. à com
poſita .65. reſiduum erit .41. hoc eſt ſum-
ma numerorum propoſitorum cum ſuis
iterationibus in ipſis partibus, quod cum
per ſe clariſſimum ſit, ſuperſluum eſt ipsam
ſummam annatomizare per ſingulas par-
tes, niſi quis habuerit eius cerebrum à fi-
gura Omega terminatum, cui tamen poſ-
ſemus dicere dictam ſummam .41. in .4.
partes diuidi, cuius prima eſſet .2. pro ad
ditione ad ſecundam partem ſimplicium,
dendus ſit .100. in quinque partes, tales
verò, quod ſecunda duplo maior ſit prima
cum .2. ſimul, tertia autem æqualis ſit pri-
mæ & ſecundæ cum .3. vnitatibus iunctis,
quarta poſteà maior ſit prima ſecunda, &
tertia per .4. vnitates, quinta demum ſu-
peret reliquas omnes per quinque vnita
tes, vt in figura .E. videre eſt, quæ quidem
partes compoſitæ (ſumpta vnitate pro
prima) ita diſpoſitæ erunt .1. 4. 8. 17. 35.
quarum ſumma erit .65. ſimplices autem
cum diſpoſitæ fuerint erunt .1. 2. 3. 6. 12.
quarum ſumma erit .24. dempta igitur
cum fuerit hæc ſimplex ſumma .24. à com
poſita .65. reſiduum erit .41. hoc eſt ſum-
ma numerorum propoſitorum cum ſuis
iterationibus in ipſis partibus, quod cum
per ſe clariſſimum ſit, ſuperſluum eſt ipsam
ſummam annatomizare per ſingulas par-
tes, niſi quis habuerit eius cerebrum à fi-
gura Omega terminatum, cui tamen poſ-
ſemus dicere dictam ſummam .41. in .4.
partes diuidi, cuius prima eſſet .2. pro ad
ditione ad ſecundam partem ſimplicium,

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib