132120IO. BAPT. BENED.
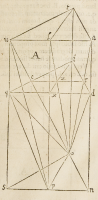
Pro cuius rei ſpeculatione imaginemur in figura corporea .A: q.a. eſſe figuram re-
ctangulam orizontalemque; ad degradandam ſuper aliquod planum perpendiculare
orizonti, & cum eo primum coniunctam in linea .q.d. cuius plani triangulum .i.q.d.
pars erit, ſit autem oculus reſpicientis .o. cuius altitudo .o.p. ab orizonte, qui quidem
conſpicit rectangulum dictum orizontale .q.a. in pyramide .o.q: o.u: o.a. et .o.d.
terminata quatuor triangulis .o.q.u: o.u.a: o.a.d. et .o.d.q. ſit verò primum ita
collocatus pes .p. eius qui reſpicit, vt linea .p.l. perpendicularis ipſi .u.a. lateri re-
ctanguli, medio loco poſita ſit, inter .a.n. et .u.s. Idque; primum nobis erit exem-
plum.
ctangulam orizontalemque; ad degradandam ſuper aliquod planum perpendiculare
orizonti, & cum eo primum coniunctam in linea .q.d. cuius plani triangulum .i.q.d.
pars erit, ſit autem oculus reſpicientis .o. cuius altitudo .o.p. ab orizonte, qui quidem
conſpicit rectangulum dictum orizontale .q.a. in pyramide .o.q: o.u: o.a. et .o.d.
terminata quatuor triangulis .o.q.u: o.u.a: o.a.d. et .o.d.q. ſit verò primum ita
collocatus pes .p. eius qui reſpicit, vt linea .p.l. perpendicularis ipſi .u.a. lateri re-
ctanguli, medio loco poſita ſit, inter .a.n. et .u.s. Idque; primum nobis erit exem-
plum.
Imaginemur nunc lineas .u.q. et .a.d. indefinitè productas eſſe, quæ in ſuperficie-
bus duorum triangulorum .o.u.q. et .o.a.d. & rectanguli orizontalis .q.a. ex prima
vndecimi Euclid. poſitæ erunt. Imaginemur etiam lineam .p.s.n. perpendicula-
rem ipſi .p.l. quæ etiam cum duabus .u.q.s. et .a.d.n. ex .34. primi Euclid. angulos
rectos conſtituet, cum ex .28. duæ .u.q.s. et .a.d.n. ſint parallelæ ipſi .p.l. et .s.n. ipſi .u.
a. & quia ſupponitur .o.p. perpendicularis plano orizontali, Angulus ergò .o.p.l. re-
ctus erit ex ſecunda definitione .11. Euclid. Imaginemur quoque ductas eſſe
duas .o.s. et .o.n. vnde .l.p. ei ſuperficiei, in qua ſunt duæ lineæ .o.p. et .s.n. ex .4.
11. perpendicularis erit, & ſuperficies orizontalis .a.s. perpendicularis erit cum dicta
o.s.n. ex .18. eiuſdem lib. vnde ex dicta definitione .o.s.u. et .o.n.a. erunt anguli recti
et .o.s. et .o.n. ex communi ſcientia, in ſuperficiebus duorum triangulorum .o.u.q. et .
o.a.d. erunt, ſi noluerimus cogere aduerſarium ad confitendum duas lineas rectas in-
cludere ſuperficiem, quemadmodum cogere-
 179[Figure 179]
tur facere, ſi opinaretur duas alias rectas per
179[Figure 179]
tur facere, ſi opinaretur duas alias rectas per
eadem puncta .o.s.n. tranſire, quæſunt in di-
ctis ſuperficiebus. Vnde .o.s. et .o.n. communes
erunt ſectiones duarum dictarum ſuperficierum
cum ſuperficie .o.s.n. Imaginemur nunc has
duas ſuperficies .o.u. et .o.a. quarum commu-
nis ſectio ſit .o.t. (quæ erit linea recta ex .3. lib.
II.) quæ erunt perpendiculares ſuperficiei .o.s.
n. ex .4. et .14. iam dictis. & ex .19. eiuſdem
o.t. perpendicularis eidem ſuperficiei .o.s.n.
erit, & ex .6. eiuſdem hæc linea .o.t. duabus .u.
q.s. et .a.d.n. parallela exiſter, & ex .9. eiuſdem
hæc linea .o.t. duabus .u.q.s. et .a.d.n. parallela
exiſtet, & ex eadem .9. erit parallela ipſi .p.l.
Imaginemur nunc planum, ſuper quod deſide
remus videre quadrangulum orizontale, quod
planum, exempli gratia, ſit primo, vt iam dixi-
mus, locatum in linea .q.d. ad angulos rectos
cum plano orizontali, cuius communes ſectio
nes cum ſuperficiebus .s.t. et .n.t. viſionis la-
terum .u.q. et .a.d. ſint .i.q. et .i.d. & com-
munis ſectio trianguli .o.u.a. ideſt viſionis
lateris .a.u. cum dicto plano, ſit .r.e. Vnde ex
communi ſcientia rectangulum orizontale,
oculo .o. ſeipſum patefaciet in plano .i.q.d. ſe-
bus duorum triangulorum .o.u.q. et .o.a.d. & rectanguli orizontalis .q.a. ex prima
vndecimi Euclid. poſitæ erunt. Imaginemur etiam lineam .p.s.n. perpendicula-
rem ipſi .p.l. quæ etiam cum duabus .u.q.s. et .a.d.n. ex .34. primi Euclid. angulos
rectos conſtituet, cum ex .28. duæ .u.q.s. et .a.d.n. ſint parallelæ ipſi .p.l. et .s.n. ipſi .u.
a. & quia ſupponitur .o.p. perpendicularis plano orizontali, Angulus ergò .o.p.l. re-
ctus erit ex ſecunda definitione .11. Euclid. Imaginemur quoque ductas eſſe
duas .o.s. et .o.n. vnde .l.p. ei ſuperficiei, in qua ſunt duæ lineæ .o.p. et .s.n. ex .4.
11. perpendicularis erit, & ſuperficies orizontalis .a.s. perpendicularis erit cum dicta
o.s.n. ex .18. eiuſdem lib. vnde ex dicta definitione .o.s.u. et .o.n.a. erunt anguli recti
et .o.s. et .o.n. ex communi ſcientia, in ſuperficiebus duorum triangulorum .o.u.q. et .
o.a.d. erunt, ſi noluerimus cogere aduerſarium ad confitendum duas lineas rectas in-
cludere ſuperficiem, quemadmodum cogere-
eadem puncta .o.s.n. tranſire, quæſunt in di-
ctis ſuperficiebus. Vnde .o.s. et .o.n. communes
erunt ſectiones duarum dictarum ſuperficierum
cum ſuperficie .o.s.n. Imaginemur nunc has
duas ſuperficies .o.u. et .o.a. quarum commu-
nis ſectio ſit .o.t. (quæ erit linea recta ex .3. lib.
II.) quæ erunt perpendiculares ſuperficiei .o.s.
n. ex .4. et .14. iam dictis. & ex .19. eiuſdem
o.t. perpendicularis eidem ſuperficiei .o.s.n.
erit, & ex .6. eiuſdem hæc linea .o.t. duabus .u.
q.s. et .a.d.n. parallela exiſter, & ex .9. eiuſdem
hæc linea .o.t. duabus .u.q.s. et .a.d.n. parallela
exiſtet, & ex eadem .9. erit parallela ipſi .p.l.
Imaginemur nunc planum, ſuper quod deſide
remus videre quadrangulum orizontale, quod
planum, exempli gratia, ſit primo, vt iam dixi-
mus, locatum in linea .q.d. ad angulos rectos
cum plano orizontali, cuius communes ſectio
nes cum ſuperficiebus .s.t. et .n.t. viſionis la-
terum .u.q. et .a.d. ſint .i.q. et .i.d. & com-
munis ſectio trianguli .o.u.a. ideſt viſionis
lateris .a.u. cum dicto plano, ſit .r.e. Vnde ex
communi ſcientia rectangulum orizontale,
oculo .o. ſeipſum patefaciet in plano .i.q.d. ſe-

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib