138126IO. BAPT. BENED.
æqualis ſit ipſi .b.c.)
 190[Figure 190]
o.m. etiam .i.c: et .f.
190[Figure 190]
o.m. etiam .i.c: et .f.
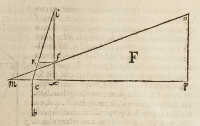
k. vt in figura .F. cla
riſſimè patet. Alias
autem multas lineas in
alijs figuris non aliam
ob camm duxi, quam ad
facilius eruendas è te-
nebris ignorantiæ, &
in cognitionis lucem
proferendas horum
effectuum cauſas, vt
dixi.
k. vt in figura .F. cla
riſſimè patet. Alias
autem multas lineas in
alijs figuris non aliam
ob camm duxi, quam ad
facilius eruendas è te-
nebris ignorantiæ, &
in cognitionis lucem
proferendas horum
effectuum cauſas, vt
dixi.
CAP. VI.
SEd vtlocum altitudinis, in noſtro plano perpendiculari orizonti, & ita locatum,
vt poſtremo diximus, inueniamus; duas hîc ſubſcriptas figuras conſiderabimus .
G. corpoream, & G. ſuperficialem, ſimiles duabus .E.E. proximè præcedentibus,
in quarum corporea ſit linea .b.M. altitudinis perpendicularis orizonti. Quare ſi
deſiderabis inuenire in noſtro plano ſitum puncti .M. ideſt punctum radij .o.M. vi-
ſualis in quo ipſe radius à plano eſt diuiſus, quod ſit .R. quamuis extra triangulum
i.q.d. tibi imaginatione confige ductam eſſe lineam .p.b. quæ erit ſectio commu-
nis orizontis cum ſuperficie .o.p.b.M. quæ ſuperficies erit perpendicularis ipſi ori-
zonti ex .18. lib 11. Quòd autemnon minus .o.p. quàm.M.b. ſit in vna eademq́ue
ſuperficie dubitandum non eſt, quia ſi imaginabimur ductam eſſe lineam .p.M. ha
bebimus triangulum .o.p.b. cum triangulo .M.b.p. communibus partibus in vna ea-
demq́ue ſuperficie conſtantem, vt triangulum quoque .o.p.M. cum triangulo M.b.
o & triangulum .o.p.b. cum triangulo .o.p.M. & triangulum .M.b.p. cum triangulo .
M.b.o. Vnde cum quilibet triangulus in vnica tantum ſuperficie ſit ex .2. lib. 11. ſe-
quetur ſuperficiem .o.p.b.M. planam eſſe, & vnicam, cuius communis ſectio cum no-
ſtro plano ſit. θ.K.R. quæ perpendicularis orizonti exiſtet ex .19. lib. 11. eritq́ue pa-
rallela ipſi .i.x. ex .6. eiuſdem. Imaginare nunc erectam eſſe .m.T. æqualem ipſi .
b.M. orizonti perpendicularem, quæ extenſa erit in ſuperficie .p.t. quod ex ſe ad
conſiderandum admodum facilè, clarumq́ue exiſtit, reducendo ad impoſſibilia
quemlibet hæc negare volentem. Imaginemur quoque ductam eſſe lineam .M.
T. quæ .b.m. ex .33. primi erit parallela, quia .m.T. ęqualis .b.M. parallela eſt
ipſi .b.M. ex .6. lib. 11. præter hæc .b.m. parallela eſt ipſi .q.d. quia ſic fuit ducta
ſuperius, vnde .M.T. parallela erit ipſi .q.d. ex .9. vndecimi, & obid perpendi-
cularis erit ſuperficiei .b.t. ex .8. eiuſdem. Nunc ſit .R.V. communis ſectio trian-
guli .o.M.T. cum noſtro plano, vnde .R.V. perpendicularis erit ſuperficiei .p.t.
ex .19. lib. 11. quam ob cauſam parallela erit ipſi .q.d. ex .6. aut ex .9. eiuſdem
quia ex .6. dicta, parallela eſt ipſi .M.T. Atſi .R.V. parallela eſt ipſi .q.d.
etiam .f.K. probatum iam fuit parallelam eſſe eidem, ergo .R.V. parallela erit
ipſi .K.f. ex .30. primi, Vnde ex .34. æqualis erit ipſi .K.f. Accedamus nunc
ad figuram .G. extructam ſupra figuram .E. ſuperficialem, & erigamus .m.T. perpendi-
cularem ipſi .m.p. ſed æqualem perfectæ altitudini, & ducamus .T.o. vt ſecet li-
neam .i.x. in puncto .V. ab ipſo ducentes .V.R. parallelam ipſi .q.d. ducendo de-
vt poſtremo diximus, inueniamus; duas hîc ſubſcriptas figuras conſiderabimus .
G. corpoream, & G. ſuperficialem, ſimiles duabus .E.E. proximè præcedentibus,
in quarum corporea ſit linea .b.M. altitudinis perpendicularis orizonti. Quare ſi
deſiderabis inuenire in noſtro plano ſitum puncti .M. ideſt punctum radij .o.M. vi-
ſualis in quo ipſe radius à plano eſt diuiſus, quod ſit .R. quamuis extra triangulum
i.q.d. tibi imaginatione confige ductam eſſe lineam .p.b. quæ erit ſectio commu-
nis orizontis cum ſuperficie .o.p.b.M. quæ ſuperficies erit perpendicularis ipſi ori-
zonti ex .18. lib 11. Quòd autemnon minus .o.p. quàm.M.b. ſit in vna eademq́ue
ſuperficie dubitandum non eſt, quia ſi imaginabimur ductam eſſe lineam .p.M. ha
bebimus triangulum .o.p.b. cum triangulo .M.b.p. communibus partibus in vna ea-
demq́ue ſuperficie conſtantem, vt triangulum quoque .o.p.M. cum triangulo M.b.
o & triangulum .o.p.b. cum triangulo .o.p.M. & triangulum .M.b.p. cum triangulo .
M.b.o. Vnde cum quilibet triangulus in vnica tantum ſuperficie ſit ex .2. lib. 11. ſe-
quetur ſuperficiem .o.p.b.M. planam eſſe, & vnicam, cuius communis ſectio cum no-
ſtro plano ſit. θ.K.R. quæ perpendicularis orizonti exiſtet ex .19. lib. 11. eritq́ue pa-
rallela ipſi .i.x. ex .6. eiuſdem. Imaginare nunc erectam eſſe .m.T. æqualem ipſi .
b.M. orizonti perpendicularem, quæ extenſa erit in ſuperficie .p.t. quod ex ſe ad
conſiderandum admodum facilè, clarumq́ue exiſtit, reducendo ad impoſſibilia
quemlibet hæc negare volentem. Imaginemur quoque ductam eſſe lineam .M.
T. quæ .b.m. ex .33. primi erit parallela, quia .m.T. ęqualis .b.M. parallela eſt
ipſi .b.M. ex .6. lib. 11. præter hæc .b.m. parallela eſt ipſi .q.d. quia ſic fuit ducta
ſuperius, vnde .M.T. parallela erit ipſi .q.d. ex .9. vndecimi, & obid perpendi-
cularis erit ſuperficiei .b.t. ex .8. eiuſdem. Nunc ſit .R.V. communis ſectio trian-
guli .o.M.T. cum noſtro plano, vnde .R.V. perpendicularis erit ſuperficiei .p.t.
ex .19. lib. 11. quam ob cauſam parallela erit ipſi .q.d. ex .6. aut ex .9. eiuſdem
quia ex .6. dicta, parallela eſt ipſi .M.T. Atſi .R.V. parallela eſt ipſi .q.d.
etiam .f.K. probatum iam fuit parallelam eſſe eidem, ergo .R.V. parallela erit
ipſi .K.f. ex .30. primi, Vnde ex .34. æqualis erit ipſi .K.f. Accedamus nunc
ad figuram .G. extructam ſupra figuram .E. ſuperficialem, & erigamus .m.T. perpendi-
cularem ipſi .m.p. ſed æqualem perfectæ altitudini, & ducamus .T.o. vt ſecet li-
neam .i.x. in puncto .V. ab ipſo ducentes .V.R. parallelam ipſi .q.d. ducendo de-

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib