2210IO. BAPT. BENED.
dabunt duodecim?
nempe dabunt decemocto, numerum quæſitum ſcilicet,
Tunc autem nil aliud pręſtamus quam quòd quærimus numerum ad quem ita ſe
habeant duodecim, ſicut duo ad tria. Ita etiam ſi quis quærat, cuius numeri duo
tertia ſint tres quintę, dicet, ſi tria dant quinque;, quid dabunt duo tertia? nempe da-
bunt integrum cum fracto nono. Hoc erit itaque; quęrere numerum ad quem ſic ſe
habeant duo tertia ſicut tria ad quinque;, quod manifeſtum eſt per ſe.
Tunc autem nil aliud pręſtamus quam quòd quærimus numerum ad quem ita ſe
habeant duodecim, ſicut duo ad tria. Ita etiam ſi quis quærat, cuius numeri duo
tertia ſint tres quintę, dicet, ſi tria dant quinque;, quid dabunt duo tertia? nempe da-
bunt integrum cum fracto nono. Hoc erit itaque; quęrere numerum ad quem ſic ſe
habeant duo tertia ſicut tria ad quinque;, quod manifeſtum eſt per ſe.
Eadem ratione qui ſcire vellet, cuius numeri duæ ſeptimæ, eſſent octo integra-
rum cum duabus quintis, diceret, ſi duo dant ſeptem quid dabunt octo integra cum
duabus quintis? nempe dabunt .29. integra cum duabus quintis numerum quæſi-
tum. Sic etiam qui transferre uellet fractum numerum in fractum, id perficeret
ex regula de tribus.
rum cum duabus quintis, diceret, ſi duo dant ſeptem quid dabunt octo integra cum
duabus quintis? nempe dabunt .29. integra cum duabus quintis numerum quæſi-
tum. Sic etiam qui transferre uellet fractum numerum in fractum, id perficeret
ex regula de tribus.
Exempli gratia ſi proponerentur vnde cim tertiædecimæ vnius totius, toto diui-
ſo in .13. partes, deſideraremusque; ſcire, quot partes totius eſsent vndecim tertiaedeci-
mæ, toto in .4. partes diuiſo, diceremus ſi .13. dant .11. quid dabunt quatuor? nem
pe dabunt tres quartas cum quinque; tertijsdecimis unius quartæ, hoc verò nihil aliud eſt
quam querere numerum, ad quem ſic ſe habeat totum in 4. partes diuiſum, ſicut
idem totum diuiſum in tredecim ſe habet ad undecim tertiasdecimas, Porrò ad
alia etiam multa hæc regula accommodata eſt.
ſo in .13. partes, deſideraremusque; ſcire, quot partes totius eſsent vndecim tertiaedeci-
mæ, toto in .4. partes diuiſo, diceremus ſi .13. dant .11. quid dabunt quatuor? nem
pe dabunt tres quartas cum quinque; tertijsdecimis unius quartæ, hoc verò nihil aliud eſt
quam querere numerum, ad quem ſic ſe habeat totum in 4. partes diuiſum, ſicut
idem totum diuiſum in tredecim ſe habet ad undecim tertiasdecimas, Porrò ad
alia etiam multa hæc regula accommodata eſt.
Hæc enim non ſine propoſito dicta ſunt, ſed ut quiſque; videat cauſam ſimilium ope-
rationum, quæ à practicis circa fractos numeros ſcriptæ ſunt, omnem à diuina illa
regula de tribus originem trahere ut etiam in ſequentibus videbimus.
rationum, quæ à practicis circa fractos numeros ſcriptæ ſunt, omnem à diuina illa
regula de tribus originem trahere ut etiam in ſequentibus videbimus.
THEOREMA XI.
CVr productum ex eo quod oritur in diuidente, ſemper æquale eſt numero
diuiſibili ſi queras ita accipe.
diuiſibili ſi queras ita accipe.
THEOREMA XII.
ID ipſum alia ratione contemplari licet.
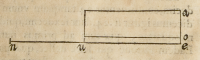
Numerus diuiſibilis ſignificetur per lineam .n.e. diuidens verò per lineam .a.e.
quod oritur linea .u.e. vnitas diuidentis .o.e. quam cogitamus eſſe vnitatem linearem;
ad hæc productum ex .u.e. in .a.e. ſit ſuperficies .u.a. Dico ſuperficiem .u.a. componi
ex tot vnitatibus ſuperficialibus quot linearibus conſtat linea .n.e. nam ex ijs quæ
diuidendi ratione notauimus, conſtituitur
eandem proportionem eſſe .n.e. ad .u.e.
 19[Figure 19]
quę eſt .a.e. ad .o.e.
At ex prima ſexti aut
19[Figure 19]
quę eſt .a.e. ad .o.e.
At ex prima ſexti aut
18. ſeptimi ſic ſe habet totale productum .
u.a. ad partiale .u.o. ſicut .a.e. ad .o.e.
quare ſic ſe habebit .u.a. ad .u.o. ſicut .n.
e. ad .u.e. ſed .u.e. et .u.o. numero non differunt, cum ſint vnius & eiuſdem ſpeciei, (ta-
met ſi numerus .u.o. ſit ſuperficialis et .u.e. linearis). Itaque; ex nona quinti numerus .
u.a. æqualis erit numero .n.e.
quod oritur linea .u.e. vnitas diuidentis .o.e. quam cogitamus eſſe vnitatem linearem;
ad hæc productum ex .u.e. in .a.e. ſit ſuperficies .u.a. Dico ſuperficiem .u.a. componi
ex tot vnitatibus ſuperficialibus quot linearibus conſtat linea .n.e. nam ex ijs quæ
diuidendi ratione notauimus, conſtituitur
eandem proportionem eſſe .n.e. ad .u.e.
18. ſeptimi ſic ſe habet totale productum .
u.a. ad partiale .u.o. ſicut .a.e. ad .o.e.
quare ſic ſe habebit .u.a. ad .u.o. ſicut .n.
e. ad .u.e. ſed .u.e. et .u.o. numero non differunt, cum ſint vnius & eiuſdem ſpeciei, (ta-
met ſi numerus .u.o. ſit ſuperficialis et .u.e. linearis). Itaque; ex nona quinti numerus .
u.a. æqualis erit numero .n.e.

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib