3018IO. BAPT. BENED.
Proponunt hi numerum in binas eiuſmodi partes diuidendum, vt ſumma qua-
dratorum dictarum partium, alteri numero poſsibili propoſito æqualis ſit, poſſi-
bili inquam, etenim ſi eiuſmodi numerus propoſitus, minor eſſet producto totius
primi in ſuum dimidium, eſſet huiuſmodi factum impoſſibile. Quod nos exequi
cupientes, ſumamus primum numerum propoſitum, quem in ſe ipſum multiplice-
mus. ab hoc quadrato deducamus ſecundum numerum propoſitum, tum quod re-
manſerit duplicemus, quod duplum denuo iubeo ex eodem primo quadrato detra-
hi, accepta poſtea radice quadrata reſidui & dempta ex priori numero propoſito,
tunc dimidium reſidui vna pars erit ex duabus primi numeri quæſita.
dratorum dictarum partium, alteri numero poſsibili propoſito æqualis ſit, poſſi-
bili inquam, etenim ſi eiuſmodi numerus propoſitus, minor eſſet producto totius
primi in ſuum dimidium, eſſet huiuſmodi factum impoſſibile. Quod nos exequi
cupientes, ſumamus primum numerum propoſitum, quem in ſe ipſum multiplice-
mus. ab hoc quadrato deducamus ſecundum numerum propoſitum, tum quod re-
manſerit duplicemus, quod duplum denuo iubeo ex eodem primo quadrato detra-
hi, accepta poſtea radice quadrata reſidui & dempta ex priori numero propoſito,
tunc dimidium reſidui vna pars erit ex duabus primi numeri quæſita.
Exempli gratia proponantur .20. diuidenda in duas eiuſmodi partes, vt ſumma
quadratorum ipſarum partium æqualis ſit .272. qui numerus maior eſt .200. maior
inquam dimidio quadrati .400. ipſorum .20. hic autem numerus .272. è quadra-
to .400. deducatur, remanebunt enim .128. quod duplicari iubeo, producentur ſiquidem .
256. quæ pariter deducta è quadrato totali, remanebunt .144. cuius radicem ſumi
volo, quæ erit .12. & dempta ex .20. priori numero dato remanebit .8. cuius di-
midium erit .4: pars vna ex quæſitis, quæ ex primo numero propoſito .20. detra-
hetur, remanebitque .16. pro altera parte.
quadratorum ipſarum partium æqualis ſit .272. qui numerus maior eſt .200. maior
inquam dimidio quadrati .400. ipſorum .20. hic autem numerus .272. è quadra-
to .400. deducatur, remanebunt enim .128. quod duplicari iubeo, producentur ſiquidem .
256. quæ pariter deducta è quadrato totali, remanebunt .144. cuius radicem ſumi
volo, quæ erit .12. & dempta ex .20. priori numero dato remanebit .8. cuius di-
midium erit .4: pars vna ex quæſitis, quæ ex primo numero propoſito .20. detra-
hetur, remanebitque .16. pro altera parte.
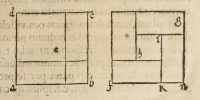
Cuius demonſtrationis cauſa, in primis cogitemus quadratum .a.c. cognitum nu-
meri .a.b. primò propoſiti, qui cogitetur diuiſus in duo quadrata .d.e. et .e.b. duo-
que ſupplementa .a.e. et .e.c. numerus autem ſummæ duorum quadratorum .d.e.
b. pro ſecundo propoſito datur; ex quo, ſumma duorum ſupplementorum .a.e.c.
conſequenter erit cognita, quę cum duplicata fuerit, & quatuor hæc ſupplementa
cogitatione accommodata, prout in
quadrato .f.g. apparet (quanuis idipſum
 39[Figure 39]
proueniret ſi modo Eucl. octaua ſecundi
39[Figure 39]
proueniret ſi modo Eucl. octaua ſecundi
aptaretur) æquali quadrato .a.c. ita vt
cogitatis quatuor ſupplementis numeri
cogniti in quadrato .f.g. ex conſequen-
ti cognoſcetur numerus quadrati partia
lis .h.i. & vna etiam eius radix qua de-
tracta ex numero .a.b. aut .f.n. (quod
idem eſt) primo propoſiti, relinquetur numerus cognitus duplum .x.k.n. aut .t.b.
pars vna totius .a.b. ex quo uerum erit hoc meum problema.
meri .a.b. primò propoſiti, qui cogitetur diuiſus in duo quadrata .d.e. et .e.b. duo-
que ſupplementa .a.e. et .e.c. numerus autem ſummæ duorum quadratorum .d.e.
b. pro ſecundo propoſito datur; ex quo, ſumma duorum ſupplementorum .a.e.c.
conſequenter erit cognita, quę cum duplicata fuerit, & quatuor hæc ſupplementa
cogitatione accommodata, prout in
quadrato .f.g. apparet (quanuis idipſum
aptaretur) æquali quadrato .a.c. ita vt
cogitatis quatuor ſupplementis numeri
cogniti in quadrato .f.g. ex conſequen-
ti cognoſcetur numerus quadrati partia
lis .h.i. & vna etiam eius radix qua de-
tracta ex numero .a.b. aut .f.n. (quod
idem eſt) primo propoſiti, relinquetur numerus cognitus duplum .x.k.n. aut .t.b.
pars vna totius .a.b. ex quo uerum erit hoc meum problema.
THEOREMA XXVIII.
SI quis & aliam rationem perficiendæ
 40[Figure 40]
huius rei quærat, hoc præſtet inuen-
40[Figure 40]
huius rei quærat, hoc præſtet inuen-
to numero huius ſupplementi, cum in
præcedenti theoremate dictum fuerit,
qua ratione manifeſtetur duplum ſupple-
menti ipſius.
to numero huius ſupplementi, cum in
præcedenti theoremate dictum fuerit,
qua ratione manifeſtetur duplum ſupple-
menti ipſius.
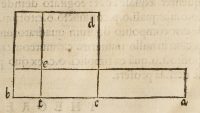
Cogitemus in ſubſcripta figura lineam .
a.b. tanquam primum numerum propoſi-
tum, & productum .a.e. ſupplemento .a.e. primæ præcedentis figuræ æquale ſit,
ac deinde ordine ab antiquis tradito procedatur, ad quadratum reducto dimidio .
a.b. videlicet .b.c. quod erit .b.d. ex quo detrahatur deinde .a.e. quare remane-
a.b. tanquam primum numerum propoſi-
tum, & productum .a.e. ſupplemento .a.e. primæ præcedentis figuræ æquale ſit,
ac deinde ordine ab antiquis tradito procedatur, ad quadratum reducto dimidio .
a.b. videlicet .b.c. quod erit .b.d. ex quo detrahatur deinde .a.e. quare remane-

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib