328316IO. BAPT. BENED.
lum, cuius data ſit b aſis tantummodo ſimul cum angulo, qui ipſi baſi opponitur.
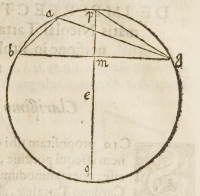
Imagineris igitur triangulum datum eſſe obtuſiangulum .a.b.g. cuius baſi .b.
g. ſit nobis data ſimul cum angulo .a. ei oppoſito, obtuſoq́ue; Conſidera etiam cir-
culum .a.b.g.q. ipſum trian gulum circunſcribentem, cuius diameter .q.e.p. tranſeat
per .m. punctum medium ipſius .b.g. tunc protractis imaginatione .e.g. et .g.p. certi eri-
mus angulos. circa .m. rectos eſſe ex .3 tertij Eucli. angulumque .q.e.g. duplum eſſe an
gulo .q.p.g. ex .19. eiuſdem, vnde æqualem angulo .a. qui etiam duplus eſt angulo .q.
p.g. quapropter proportio arcus .q.g. ad arcum
 350[Figure 350]
g.p. tibi cognita erit, & proportio etiam chor-
350[Figure 350]
g.p. tibi cognita erit, & proportio etiam chor-
de .p.g. ad ſinum .m.g. arcus .g.p. & quia .m.g. vt
dimidium ipſius .b.g. tibi data eſt, cognoſces
etiam .p.g. vt .m.g. & ſic tertium latus .m.p. trian-
guli orthogonij .p.m.g. & qa ex .34. tertij quod
fit ex .p.m. in .m.q. eſt æquale ei quod fit ex .b.m.
in .m.g. ideo cum diuiſum fuerit productum .b.
m in .m.g. per .p.m. proueniet .m.q. quapropter
habebis totum .q.p.
g. ſit nobis data ſimul cum angulo .a. ei oppoſito, obtuſoq́ue; Conſidera etiam cir-
culum .a.b.g.q. ipſum trian gulum circunſcribentem, cuius diameter .q.e.p. tranſeat
per .m. punctum medium ipſius .b.g. tunc protractis imaginatione .e.g. et .g.p. certi eri-
mus angulos. circa .m. rectos eſſe ex .3 tertij Eucli. angulumque .q.e.g. duplum eſſe an
gulo .q.p.g. ex .19. eiuſdem, vnde æqualem angulo .a. qui etiam duplus eſt angulo .q.
p.g. quapropter proportio arcus .q.g. ad arcum
de .p.g. ad ſinum .m.g. arcus .g.p. & quia .m.g. vt
dimidium ipſius .b.g. tibi data eſt, cognoſces
etiam .p.g. vt .m.g. & ſic tertium latus .m.p. trian-
guli orthogonij .p.m.g. & qa ex .34. tertij quod
fit ex .p.m. in .m.q. eſt æquale ei quod fit ex .b.m.
in .m.g. ideo cum diuiſum fuerit productum .b.
m in .m.g. per .p.m. proueniet .m.q. quapropter
habebis totum .q.p.
Idem efficies, ſi cum angulus .a. acutus fuiſſet.
Modus inueniendi puncta elliptica via Pergei.
AD EVNDEM.
MOdus inueniendi puncta elliptica, via .21. primi lib. Pergei ex datis axibus,
vt vbi alias ſignificati, talis eſt.
 351[Figure 351]
Sit exempli gratia maior axis propo-
351[Figure 351]
Sit exempli gratia maior axis propo-
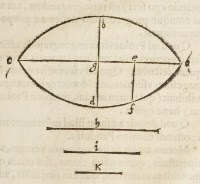
ſitus .a.c. minor autem .b.d. cum ergo
volueris inuenire punctum circunfe-
rentiæ correſpondentem puncto .e.
maioris axis, inueniemus primò la-
tus tetragonicum producti .a.g. in .g.
c. quod ſit .h. latusque tetragonicum pro-
ducti .a.e. in .e.c. quod ſit .i. deinde in-
ueniemus lineam .K. tertiam in con-
tinua proportionalitate cum .h. et .i.
vnde .i. erit media proportionalis in-
ter .h. et .K. & vt .h. proportionalis erit
ad .K. inueniemus .e.f. cui .g.d. medie-
tas ſecundi axis ita ſe habeat, quæ po
ſtea iuncta axi maiori, ad angulosrectos in puncto .e. dabit ſitum puncti .f. quæſiti ex
dicta .21. primi lib. Pergei, ſed talis modus prolixus eſt.
vt vbi alias ſignificati, talis eſt.
ſitus .a.c. minor autem .b.d. cum ergo
volueris inuenire punctum circunfe-
rentiæ correſpondentem puncto .e.
maioris axis, inueniemus primò la-
tus tetragonicum producti .a.g. in .g.
c. quod ſit .h. latusque tetragonicum pro-
ducti .a.e. in .e.c. quod ſit .i. deinde in-
ueniemus lineam .K. tertiam in con-
tinua proportionalitate cum .h. et .i.
vnde .i. erit media proportionalis in-
ter .h. et .K. & vt .h. proportionalis erit
ad .K. inueniemus .e.f. cui .g.d. medie-
tas ſecundi axis ita ſe habeat, quæ po
ſtea iuncta axi maiori, ad angulosrectos in puncto .e. dabit ſitum puncti .f. quæſiti ex
dicta .21. primi lib. Pergei, ſed talis modus prolixus eſt.

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib