340328IO. BAPT. BENED.
zonte;
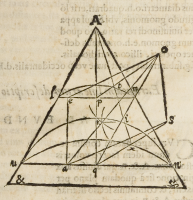
cogitemus etiam lineam .A.t.i.x. illud coni latus eſſe, qu od à ſummitate ver
ſus baſim tranſit per medium latitudinis ipſius gnomonis, concipiamus etiam mente
e.a. communem ſectionem eſſe trianguli ſupra dicti cum azimut horæ, necnon pun-
ctum .K. eſſe commune radio Solis .o.a. & ſuperficiei conicæ, quod quidem eſt illud
quod quæritur, hoc ſcilicet modo. Primum cognoſcimus angulum .p.A.t. vt medie
tas anguli totius coni, & angulum .p. rectum, vnde .t. tam intrinſecus, quam extrinſe-
custrianguli .A.p.t. nobis cognitus erit. Nunc cum angulus .A.t.o. cognoſcatur, ſi
gnomon t.o. fixus fuerit in ſuperficie conica, ita qd cum latere .A.t. eſſiciat angulum
A.t.o. & lateraliter faciat angulosrectos cum ſuperficie conica, ad quod efficiendum
nulla eſt difficultas, cognoſcendo deinde .A.t. ſimul cum angulis .A. et .t. intrinſecis
trianguli ortogonij .A.p.t. cognoſcemus .p.t. et .A.p. vnde etiam tota .o.p. ſed cogno
ſcendo .o.p. cum angulo .p.o.e. (angulus enim .p.o.e. cognoſcitur ex hypotheſi cum
ſit inter azimut Solis & azimut gnomonis) cum angulo .o.p.e. recto cognoſcemus .p.
e. et .o.e. deinde cum nobis nota ſit .o.e. cum angulo altitudinis Solis .e.o.a. & angu-
lo .o.e.a. recto cognoſc emus longitudinem azimutalis .e.a. necnon quantitatem .a.o.
Imaginata poſtea .a.q. æquidiſtante .e.p. habebimus .p.q. æqualem .a.e. ex .34. primi
Eucli. Vnde duabus .o.p. et .p.q. mediantibus, cognitiſque; cum angulo recto .p. cogno
ſcemus .o.q. nec non angulum .o.q.
p. quo mediante, necnon median-
te angulo .q.A.t. et .A.q. cognita, co
 363[Figure 363]
gnoſcemus .A.i. et .q.i. quę .q.i. dem
363[Figure 363]
gnoſcemus .A.i. et .q.i. quę .q.i. dem
pta à .q.o. relinquet nobis cognitam
i.o. Et quia .o.i.q. et .o.K.a. ſemper
ſunt in eadem ſuperficie ſecante co
num, quæ etiam ſecat ſuperficiem
trianguli .A.q.x. ad rectos ex .18. vn
decimi, cum linea .u.n. perpendicu
laris ſit ſuperficiei trianguli .A.q.i.
ex .8. dicti, quia parallela eſt .l.p. quę
perpendicularis eſt ſuperficiei trian-
guli .o.p.q. ex .4. eiuſdem, ſequitur,
quod talis ſectio ( quæ intelligatur
per .u.K.i.n.) ſemper erit elliptica,
vel parabole, ſeu hyperbole, prout
linea .o.i.q. ſecabit latus coni, oppo
ſitum lateri .A.i. diſtento in ipſa ſuperficie conica, ſeu ad ſuperiorem partem produ
ctum, velipſi parallelum.
ſus baſim tranſit per medium latitudinis ipſius gnomonis, concipiamus etiam mente
e.a. communem ſectionem eſſe trianguli ſupra dicti cum azimut horæ, necnon pun-
ctum .K. eſſe commune radio Solis .o.a. & ſuperficiei conicæ, quod quidem eſt illud
quod quæritur, hoc ſcilicet modo. Primum cognoſcimus angulum .p.A.t. vt medie
tas anguli totius coni, & angulum .p. rectum, vnde .t. tam intrinſecus, quam extrinſe-
custrianguli .A.p.t. nobis cognitus erit. Nunc cum angulus .A.t.o. cognoſcatur, ſi
gnomon t.o. fixus fuerit in ſuperficie conica, ita qd cum latere .A.t. eſſiciat angulum
A.t.o. & lateraliter faciat angulosrectos cum ſuperficie conica, ad quod efficiendum
nulla eſt difficultas, cognoſcendo deinde .A.t. ſimul cum angulis .A. et .t. intrinſecis
trianguli ortogonij .A.p.t. cognoſcemus .p.t. et .A.p. vnde etiam tota .o.p. ſed cogno
ſcendo .o.p. cum angulo .p.o.e. (angulus enim .p.o.e. cognoſcitur ex hypotheſi cum
ſit inter azimut Solis & azimut gnomonis) cum angulo .o.p.e. recto cognoſcemus .p.
e. et .o.e. deinde cum nobis nota ſit .o.e. cum angulo altitudinis Solis .e.o.a. & angu-
lo .o.e.a. recto cognoſc emus longitudinem azimutalis .e.a. necnon quantitatem .a.o.
Imaginata poſtea .a.q. æquidiſtante .e.p. habebimus .p.q. æqualem .a.e. ex .34. primi
Eucli. Vnde duabus .o.p. et .p.q. mediantibus, cognitiſque; cum angulo recto .p. cogno
ſcemus .o.q. nec non angulum .o.q.
p. quo mediante, necnon median-
te angulo .q.A.t. et .A.q. cognita, co
pta à .q.o. relinquet nobis cognitam
i.o. Et quia .o.i.q. et .o.K.a. ſemper
ſunt in eadem ſuperficie ſecante co
num, quæ etiam ſecat ſuperficiem
trianguli .A.q.x. ad rectos ex .18. vn
decimi, cum linea .u.n. perpendicu
laris ſit ſuperficiei trianguli .A.q.i.
ex .8. dicti, quia parallela eſt .l.p. quę
perpendicularis eſt ſuperficiei trian-
guli .o.p.q. ex .4. eiuſdem, ſequitur,
quod talis ſectio ( quæ intelligatur
per .u.K.i.n.) ſemper erit elliptica,
vel parabole, ſeu hyperbole, prout
linea .o.i.q. ſecabit latus coni, oppo
ſitum lateri .A.i. diſtento in ipſa ſuperficie conica, ſeu ad ſuperiorem partem produ
ctum, velipſi parallelum.
Supponamus nunc dictam lineam .o.q. ſecare dictum oppoſitum latus lateri .A.i.
verſus baſim, vnde ſectio .u.K.i.n. erit elliptica. quod facile cognitu eſt mediante com
paratione angulorum .A.q.i. et .q.A.i. interſe, eo quod ſi eſſent ęquales, dicta ſect o
barabola eſſet ex .27. primi Eucli. et .11. primi Pergei, ſed ſi angulus .A.q.i. maior eſ-
ſet angulo .q.A.i. ſectio eſſet ellipſis, ex ultimo poſtulato primi Euclid. & ex .13. pri-
mi Pergei, ſed ſi dictus angulus .A.q.i. minor eſſet angulo .A. tunc ſectio eſſet hyper-
bole ex dicto poſtulato & ex .12. primi Pergei. Sit ergo primum vt dictum eſt, hoc
eſt, quod ſectio eſſet oxygonia, ideſt elliptica, ſeu defectio (quod idem eſt,) ſepa-
ratim oportebit nos ellipſim deſignare ſimilem ęqualemque; ei, quæ eſt .u.K.i.n. quod quidem
difficile non erit, quotieſcunque ſuos axes inuenerimus, maiorem ſcilicet, & mino-
verſus baſim, vnde ſectio .u.K.i.n. erit elliptica. quod facile cognitu eſt mediante com
paratione angulorum .A.q.i. et .q.A.i. interſe, eo quod ſi eſſent ęquales, dicta ſect o
barabola eſſet ex .27. primi Eucli. et .11. primi Pergei, ſed ſi angulus .A.q.i. maior eſ-
ſet angulo .q.A.i. ſectio eſſet ellipſis, ex ultimo poſtulato primi Euclid. & ex .13. pri-
mi Pergei, ſed ſi dictus angulus .A.q.i. minor eſſet angulo .A. tunc ſectio eſſet hyper-
bole ex dicto poſtulato & ex .12. primi Pergei. Sit ergo primum vt dictum eſt, hoc
eſt, quod ſectio eſſet oxygonia, ideſt elliptica, ſeu defectio (quod idem eſt,) ſepa-
ratim oportebit nos ellipſim deſignare ſimilem ęqualemque; ei, quæ eſt .u.K.i.n. quod quidem
difficile non erit, quotieſcunque ſuos axes inuenerimus, maiorem ſcilicet, & mino-

 zoom in
zoom in
 zoom out
zoom out
 zoom area
zoom area
 full page
full page
 page width
page width
 set mark
set mark
 remove mark
remove mark
 get reference
get reference
 digilib
digilib